【剑指offer】7：斐波那契数列

题目描述：

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。假设 n≤39

解题思路：

斐波拉契数列：1,1,2,3,5,8……，总结起来就是第一项和第二项的值均为1，后续的第n项的值为（n-1）与（n-2）项值的和。

公式总结为：

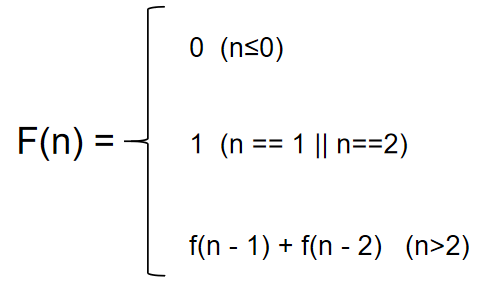
由以上公式不难看出，本题可以直接用递归方式进行解决，但是，会出现一个严重的效率问题。以f（8）为例子，若想求出f（8）的值需要先知道f（7）和f（6）的值，同样，若想知道f（7）则需要知道f（6）和f（5）的值，以此类推，当n的值越大，需要进行的重复运算越多，导致严重的效率问题。

因此，我们不妨直接用循环解决问题：

代码实现

（C实现）：

int Fibonacci(int n) {
    if (n <= 0) return 0;
    if (n == 1 || n == 2) return 1;
    //  return  Fibonacci(n - 1) + Fibonacci(n - 2);     递归只需要这一句
    int fir = 1, sec = 1, res = 0;
    for (int i = 2; i < n; i++)
    {
        res = fir + sec;
        fir = sec;
        sec = res;
    }
    return res;
}

（JavaScript实现）：

function Fibonacci(n) {
    var fir = 1, sec = 1, res;
    if (n <= 0) {
        return 0;
    }else if (n == 1 || n == 2) {
        return 1;
    }
    //  return  Fibonacci(n - 1) + Fibonacci(n - 2);  递归只需要这一句
    for (var i = 2; i < n; i++) {
        res = fir + sec;
        fir = sec;
        sec = res;
    }
    return res;
}