【题解】JSOIWC2019 Round1

题面（T1变成5s（毒瘤出题人发现std超时了qaq））：

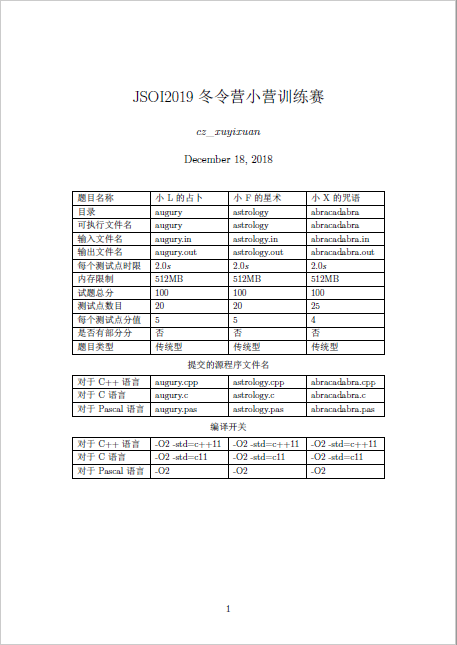
啥都不会qaq。但也送了不少分

题解：

T1:

当T=0时直接异或前缀和，但T=1时就有点恶心

暴力能有80pts（防止大家爆零）

还珂以用莫队，期望得分90_{95pts，不比暴力好多少（所以窝考场上没敲）}~

T=1时正解是整解是树状数组维护区间不同元素的异或和

先将询问离线按照左排序

再用T=0时的异或前缀和再异或上树状数组中保存的值，就是答案

完整程序

#include <bits/stdc++.h>
#define N 1000005
using namespace std;
inline int read()
{
    register int x=0,f=1;register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*f;
}
inline void write(register int x)
{
    if(!x)putchar('0');if(x<0)x=-x,putchar('-');
    static int sta[20];register int tot=0;
    while(x)sta[tot++]=x%10,x/=10;
    while(tot)putchar(sta[--tot]+48);
}
struct BinaryIndexTree{
	int n,a[N];
	inline void init(register int x)
	{
		n=x;
		memset(a,0,sizeof(a));
	}
	inline void modify(register int x,register int d)
	{
		for(register int i=x;i<=n;i+=i&-i)
			a[i]^=d;
	}
	inline int query(register int x)
	{
		int ans=0;
		for(register int i=x;i;i-=i&-i)
			ans^=a[i];
		return ans;
	}
}BIT;
int n,m,a[N],s[N],ans[N],next[N];
bool flag[N];
vector <pair<int,int> > q[N];
map<int,int> last;
int main()
{
//	freopen("augury.in","r",stdin);
//	freopen("augury.out","w",stdout);
	int num=read();
	n=read(),m=read();
	for(register int i=1;i<=n;++i)
	{
		a[i]=read();
		s[i]=s[i-1]^a[i];
	}
	for(register int i=1;i<=m;++i)
	{
		int l=read(),r=read(),t=read();
		if(!t)
			ans[i]=s[r]^s[l-1];
		else
			q[l].push_back(make_pair(r,i));
	}
	for(register int i=n;i;--i)
	{
		next[i]=last[a[i]];
		flag[next[i]]=true;
		last[a[i]]=i;
	}
	BIT.init(n);
	for(register int i=1;i<=n;++i)
		if(!flag[i])
			BIT.modify(i,a[i]);
	for(register int i=1;i<=n;++i)
	{
		for(register int j=0;j<q[i].size();++j)
			ans[q[i][j].second]=s[q[i][j].first]^s[i-1]^BIT.query(q[i][j].first);
		BIT.modify(i,a[i]);
		if(next[i])
			BIT.modify(next[i],a[i]);
	}
	for(register int i=1;i<=m;++i)
		write(ans[i]),puts("");
	return 0;
}

T2

神仙期望题（我肯定不会），题意也没读懂，下次再研究吧

打表有10pts，但出题人有反打表系统

先是树形dp，求k条链不相交的总数

最后算期望

std：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5005;
const int P = 998244353;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n, size[MAXN], dp[MAXN][MAXN][3];
vector <int> a[MAXN];
void update(int &x, int y) {
	x += y;
	if (x >= P) x -= P;
}
void work(int pos, int fa) {
	size[pos] = 1;
	dp[pos][1][0] = dp[pos][0][2] = 1;
	for (auto x : a[pos])
		if (x != fa) {
			work(x, pos);
			static int res[MAXN][3];
			for (int i = 1; i <= size[pos] + size[x]; i++)
				res[i][0] = res[i][1] = res[i][2] = 0;
			for (int i = 0; i <= size[pos]; i++)
			for (int j = 0; j <= size[x]; j++) {
				update(res[i + j][0], 1ll * dp[pos][i][0] * dp[x][j][0] % P);
				if (i + j) update(res[i + j - 1][1], 1ll * dp[pos][i][0] * dp[x][j][0] % P);
				update(res[i + j][0], 1ll * dp[pos][i][0] * dp[x][j][1] % P);
				if (i + j) update(res[i + j - 1][1], 1ll * dp[pos][i][0] * dp[x][j][1] % P);
				update(res[i + j][0], 1ll * dp[pos][i][0] * dp[x][j][2] % P);

				update(res[i + j][1], 1ll * dp[pos][i][1] * dp[x][j][0] % P);
				if (i + j) update(res[i + j - 1][2], 1ll * dp[pos][i][1] * dp[x][j][0] % P);
				update(res[i + j][1], 1ll * dp[pos][i][1] * dp[x][j][1] % P);
				if (i + j) update(res[i + j - 1][2], 1ll * dp[pos][i][1] * dp[x][j][1] % P);
				update(res[i + j][1], 1ll * dp[pos][i][1] * dp[x][j][2] % P);

				update(res[i + j][2], 1ll * dp[pos][i][2] * dp[x][j][0] % P);
				update(res[i + j][2], 1ll * dp[pos][i][2] * dp[x][j][1] % P);
				update(res[i + j][2], 1ll * dp[pos][i][2] * dp[x][j][2] % P);
			}
			for (int i = 1; i <= size[pos] + size[x]; i++) {
				dp[pos][i][0] = res[i][0];
				dp[pos][i][1] = res[i][1];
				dp[pos][i][2] = res[i][2];
			}
			size[pos] += size[x];
		}
}
int power(int x, int y) {
	if (y == 0) return 1;
	int tmp = power(x, y / 2);
	if (y % 2 == 0) return 1ll * tmp * tmp % P;
	else return 1ll * tmp * tmp % P * x % P;
}
int main() {
	freopen("astrology.in", "r", stdin);
	freopen("astrology.out", "w", stdout);
	int num; read(num); read(n);
	for (int i = 1; i <= n - 1; i++) {
		int x, y; read(x), read(y);
		a[x].push_back(y);
		a[y].push_back(x);
	}
	work(1, 0);
	int ans = 1, tot = ((dp[1][1][1] + dp[1][1][2]) % P + dp[1][1][0]) % P;
	int fac = 1, frac = 1;
	for (int i = 1; i <= n; i++) {
		fac = 1ll * fac * i % P;
		frac = 1ll * frac * tot % P;
		int now = ((dp[1][i][1] + dp[1][i][2]) % P + dp[1][i][0]) % P;
		update(ans, 1ll * now * fac % P * power(frac, P - 2) % P);
	}
	writeln(ans);
	return 0;
}

T3

也有反打表系统qaq（打表有20pts）

正解也不会啊，我就放一下官方题解吧qaq

这题是是有向图计数

std:

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int n, P, ans, c[MAXN][MAXN], fac[MAXN], inv[MAXN], two[MAXN];
void update(int &x, int y) {
	x += y;
	if (x >= P) x -= P;
}
int sign(int x) {
	if (x & 1) return P - 1;
	else return 1;
}
int main() {
	freopen("abracadabra.in", "r", stdin);
	freopen("abracadabra.out", "w", stdout);
	int num; read(num), read(n), read(P);
	for (int i = 0; i <= n * 2; i++) {
		c[i][0] = 1;
		if (i == 0) fac[i] = two[i] = inv[i] = 1;
		else {
			fac[i] = 1ll * fac[i - 1] * i % P;
			two[i] = 2ll * two[i - 1] % P;
			inv[i] = 1ll * inv[i - 1] * (P + 1) / 2 % P;
		}
		for (int j = 1; j <= i; j++)
			c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % P;
	}
	for (int i = 0; i <= n; i++)
	for (int j = 0; j <= n - i; j++)
	for (int k = 0; k <= n - i - j; k++) {
		int coef = 1ll * sign(i + k) * c[n][i] % P * c[n - i][j] % P * c[n - i - j][k] % P * two[n - i - j] % P;
		int value = 1ll * c[i + j][j] * fac[i] % P * fac[2 * j + k] % P * inv[j] % P;
		update(ans, 1ll * coef * value % P);
	}
	writeln(1ll * ans * inv[n] % P);
	return 0;
}

深深地感受到自己的弱小~

分数太菜，80+10+20=110（反打表系统忽略了qaq），gsy他85（他输出kkksc03没被判打表qaq，wcy他65，ljd他45，cyc打表竟然有分（smog，他85

实际应该可以100+10+20=130的，还是太菜啊

简单的树状数组都写不出

深深地感受到自己的弱小~