整理一点与排列组合有关的问题[组合数 Stirling数 Catalan数]

都是数学题

思维最重要，什么什么数都没用，DP直接乱搞(雾..

参考LH课件，以及资料：http://daybreakcx.is-programmer.com/posts/17315.html

做到有关的题目会更新

---

n个乒乓球放到m个盒子里的方案数

1.球相同，盒子不同，不允许空

分成m段，n-1个空选m-1个放隔板 ，$\binom{n-1}{m-1}$

2.球相同，盒子不同，允许空

$(1)$ 加入m个球变成不允许空

$(2)$ m-1个隔板和球放在一起，从中选m-1个做隔板

$C_{n+m-1}^{m-1}$

3.球相同，盒子相同，不允许空

就是整数划分问题啊...n个数写成m个数的和的形式的方案数

$ f[i][j]=f[i-1][j-1]+f[i-j][j] $

有1的话就是$ f[i-1][j-1]$，没有1的话就拿出j个1先放上再分剩下的，$f[i-j][j]$

或者直接写暴力转移然后化简

4.球相同，盒子相同，允许空

$ \sum_{j=1}^mf[n][j] $

5.球不同，盒子相同，不允许空

第二类Stirling数：n个不同的元素分成m个集合的方案数

$ S(i,j)=S(i-1,j-1)+S(i-1,j)*j $

$ S(n,n)=1 \quad n \ge 0\quad,\quad S(n,0)=0 , n\ge 1$

考虑一个元素可以放入一个空集合或者已经有元素的集合(j种选择)

6.球不同，盒子相同，允许空

枚举非空盒子数量

$ \sum_{j=1}^mS(n,j) $

7.球不同，盒子不同，不允许空

盒子全排列标号就行了

$S(n,m)*m!$

8.球不同，盒子不同，允许空

不能简单的全排列标号，因为空盒子标号没有意义

所以枚举非空盒子数量的时候乘上个组合数和全排列标号

$ \sum_{j=1}^m{S(n,j)*C_{m}^{j}*j!} $

---

n个球选m个，不能选相邻的

拿出球后会留下空

把选的拿出来，剩下n-m个球n-m+1个空(包括两端)，再把拿出来的m个插到空里去

$ C_{n-m+1}^{m}$

---

把n颗珍珠，穿成m个项链，旋转后相同的项链是一种项链。珍珠不同，项链相同。

第一类Stirling数：n个不同元素构成m个圆排列的方案数

$ s(i,j)=s(i-1,j-1)+s(i-1,j)*(i-1) $

$ s(n,n)=1 \quad n \ge 1\quad,\quad s(n,0)=0 $

考虑一个元素可以放入一个空排列或者某一个元素后面(i-1种选择)

---

Catalan数

[总结]：

1.卡特兰数的一个特点是问题有n点，选择某一点后分成两个子问题，两个字问题互相独立

2.或者可以直接往原始定义方向建模：每一步有两种决策，规定任意时刻一种决策数量不能超过另一种

[通项公式]：

$ C_n = \frac{1}{n+1}{2n\choose n} \quad n\ge 0 \quad C_0 = 1 \quad C_1=1$

$1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670...$

[公式变形]：

$1\quad C_n = {2n\choose n} - {2n\choose n+1} \quad$

$2\quad C_n = \frac{4n-2}{n+1} C_n-1 $

$3\quad C_{n} = \sum_{i=0}^{n-1}C_{i}*C_{n-i-1}\quad$

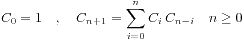
[应用]：

原始：n个+1和n个-1构成2n项$a_i$，其部分和满足$a_1+a_2+...+a_k \ge 0\quad , 0 \le k\le 2n $的序列个数等于第n个Catalan数。

证明：不合法的有${2n\choose n+1}$个，考虑第一个不合法位置$k$一定是$-1$，$1...k$正负互换后得到的序列有$n+1$个$+1$，$m-1$个$-1$，这些都是不合法的要减去

$1$ 合法括号序列方案数

　　考虑$( +1\quad  ) -1$

$2$ $n$个节点二叉树形态数

　　考虑根的左孩子和右孩子节点数

$3$ 在网格中从$(0,0)$走到$(n,n)$，只能向上或向右走，不能跨过$y=x$这条直线，方案数。

　　法1.枚举第一次走到$y=x$的位置

　　法2.一共走了$2n$次，向右 $+1$ ，向上 $-1$

$4$ 凸n边形切三角剖分(分成$n-2$个三角形)方案数

　　枚举三角形$1nj$的$j$，分成了两个多边形，乘法原理$f[i]=f[j]*f[n-j+1]$，这里的Catlan数列从$f[3]$开始,考虑整体$-2$后变成标准形式

$5$ n个数入栈后的出栈的排列方案数

　　法1.枚举最后出栈的元素，小于他的和大于他的独立，乘法原理

　　法2.一共$2n$次操作，入栈$+1$，出栈$-1$

$6$ n层的阶梯切割为n个矩形的方案数

n层阶梯有n个角，切割后每个矩形都占有一个角，一定有一个矩形占有左上角，然后分成了两个互相独立的子问题...

[一个变形]：

$+1$有$n$个，$-1$有$m$个，$n \ge m$，求方案数

和原始版本的证明思路相同，第一个不合法前面正负互换之后还是$n+1$个$+1$，方案数还是

$1\quad C_{n+m} = {{n+m}\choose n} - {{n+m}\choose n+1} \quad$

$7$ BZOJ 1485: [HNOI2009]有趣的数列