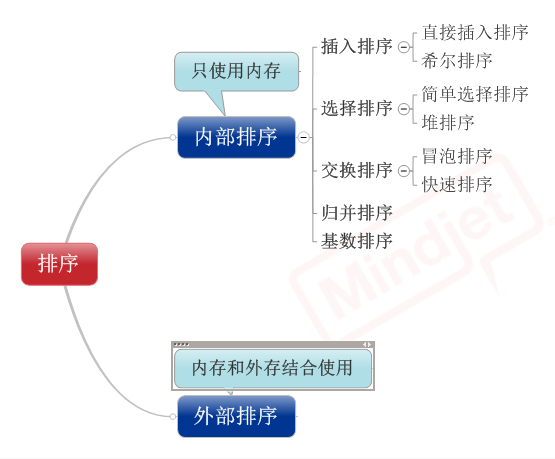
Algorithm --> 十大排序算法

十大排序算法

主要排序法有：  
一、冒泡（ Bubble）排序—— 相邻交换  
二、选择排序 ——每次最小/ 大排在相应的位置  
三、插入排序 ——将下一个插入已排好的序列中  
四、壳（ Shell）排序—— 缩小增量  
五、归并排序  
六、快速排序  (待补充)
七、堆排序  (待补充)
八、拓扑排序  (待补充)
九、锦标赛排序  (待补充)
十、基数排序  (待补充)

1、冒泡（ Bubble）排序 

基本思想：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

void BubbleSortArray()
{
    for(int i=;i<n;i++)
    {
        for(int j=;i<n-i;j++)
        {
            if(a[j]>a[j+])//比较交换相邻元素
            {
                int temp;
                temp=a[j];
                a[j]=a[j+];
                a[j+]=temp;
            }
        }
    }
} 

效率 O（ n²）, 适用于排序小列表。

2、选择排序

基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

void SelectSortArray()
{
    int min_index;
    for(int i=;i<n-;i++)
    {
        min_index=i;
        for(int j=i+;j<n;j++)//每次扫描选择最小项
        {
              if(arr[j]<arr[min_index])
                min_index=j;
        }
        if(min_index!=i)//找到最小项交换，即将这一项移到列表中的正确位置
        {
            int temp;
            temp=arr[i];
            arr[i]=arr[min_index];
            arr[min_index]=temp;
        }
    }
} 

效率O（ n²），适用于排序小的列表。

3、 插入排序

基本思想：在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

void InsertSortArray()
{
    for(int i=;i<n;i++)//循环从第二个数组元素开始，因为 arr[0]作为最初已排序部分
    {
        int temp=arr[i];//temp标记为未排序第一个元素
        int j=i-;
        while (j>= && arr[j]>temp)/*将 temp与已排序元素从小到大比较，寻找 temp应插入的位置*/
        {
            arr[j+]=arr[j];
            j--;
        }
        arr[j+]=temp;
    }
} 

最佳效率 O（n ）；最糟效率 O（n² ）与冒泡、选择相同，适用于排序小列表，若列表基本有序，则插入排序比冒泡、选择更有效率。

4、希尔（Shell）排序

基本思想：算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

void  ShellSortArray1()
{
    for(int incr=;incr>;incr--)//增量递减，以增量 3，2 ，1为例
    {
        for(int L=;L<(n-)/incr;L++)//重复分成的每个子列表
        {
            for(int i=L+incr;i<n;i+=incr)//对每个子列表应用插入排序
            {
                int temp=arr[i];
                int j=i-incr;
                while(j>=&&arr[j]>temp)
                {
                    arr[j+incr]=arr[j];
                    j-=incr;
                }
                arr[j+incr]=temp;
            }
        }
    }
} 

void  ShellSortArray2(int *data, int len)
{
    int d = len;
    while(d > )
    {
        d = (d+)/;
        for(int i=; i<len-d; i++)
        {
            if(data[i+d] < data[i])
            {
                int tmp = data[i+d];
                data[i+d] = data[i];
                data[i] = tmp;
            }
        }
    }
} 

适用于排序小列表。 效率估计 O（nlog2^n ）~O（ n^1.5），取决于增量值的最初大小。建议使用质数作为增量值，因为如果增量值是 的幂，则在下一个通道中会再次比较相同的元素。 壳（Shell）排序改进了插入排序，减少了比较的次数。是不稳定的排序，因为排序过程中元素可能会前后跳跃。

5、归并排序

基本思想：归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

//将有二个有序数列a[first...mid]和a[mid...last]合并。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
    int i = first, j = mid + ;
    int m = mid,   n = last;
    int k = ;  

    while (i <= m && j <= n)
    {
        if (a[i] <= a[j])
            temp[k++] = a[i++];
        else
            temp[k++] = a[j++];
    }
    while (i <= m)  temp[k++] = a[i++];
    while (j <= n)  temp[k++] = a[j++];
    for (i = ; i < k; i++)
        a[first + i] = temp[i];
} 

void mergesort(int a[], int first, int last, int temp[])
{
    if (first < last)
    {
        int mid = (first + last) / ;
        mergesort(a, first, mid, temp);    //左边有序
        mergesort(a, mid + , last, temp); //右边有序
        mergearray(a, first, mid, last, temp); //再将二个有序数列合并
    }
}  

bool MergeSort(int a[], int n)
{
    int *p = new int[n];
    if (p == NULL)  return false;
    mergesort(a, , n - , p);
    delete[] p;
    return true;
}