[LeetCode] Count Complete Tree Nodes 求完全二叉树的节点个数

Given a complete binary tree, count the number of nodes.

Note:

Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Example:

Input:
    1
   / \
  2   3
 / \  /
4  5 6

Output: 6

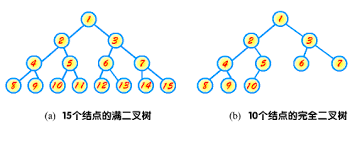
这道题给定了一棵完全二叉树，让我们求其节点的个数。很多人分不清完全二叉树和满二叉树的区别，下面让我们来看看维基百科上对二者的定义：

完全二叉树 (Complete Binary Tree)：

A Complete Binary Tree （CBT) is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；

换句话说，完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

完美二叉树 (Perfect Binary Tree)：

A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth. All internal nodes have degree 2.

二叉树的第i层至多拥有  个节点数；深度为k的二叉树至多总共有  个节点数，而总计拥有节点数匹配的，称为“满二叉树”；

完满二叉树 (Full Binary Tree):

A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.

换句话说，所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）

其实这道题的最暴力的解法就是直接用递归来统计结点的个数，根本不需要考虑什么完全二叉树还是完美二叉树，递归在手，遇 tree 不愁。直接一行搞定碉堡了，这可能是我见过最简洁的 brute force 的解法了吧，参见代码如下：

解法一：

class Solution {
public:
    int countNodes(TreeNode* root) {
        return root ? ( + countNodes(root->left) + countNodes(root->right)) : ;
    }
};

我们还是要来利用一下完全二叉树这个条件，不然感觉对出题者不太尊重。通过上面对完全二叉树跟完美二叉树的定义比较，可以看出二者的关系是，完美二叉树一定是完全二叉树，而完全二叉树不一定是完美二叉树。那么这道题给的完全二叉树就有可能是完美二叉树，若是完美二叉树，节点个数很好求，为2的h次方减1，h为该完美二叉树的高度。若不是的话，只能老老实实的一个一个数结点了。思路是由 root 根结点往下，分别找最靠左边和最靠右边的路径长度，如果长度相等，则证明二叉树最后一层节点是满的，是满二叉树，直接返回节点个数，如果不相等，则节点个数为左子树的节点个数加上右子树的节点个数再加1(根节点)，其中左右子树节点个数的计算可以使用递归来计算，参见代码如下：

解法二：

class Solution {
public:
    int countNodes(TreeNode* root) {
        int hLeft = , hRight = ;
        TreeNode *pLeft = root, *pRight = root;
        while (pLeft) {
            ++hLeft;
            pLeft = pLeft->left;
        }
        while (pRight) {
            ++hRight;
            pRight = pRight->right;
        }
        if (hLeft == hRight) return pow(, hLeft) - ;
        return countNodes(root->left) + countNodes(root->right) + ;
    }
};

我们也可以全用递归的形式来解，如下所示：

解法三：

class Solution {
public:
    int countNodes(TreeNode* root) {
        int hLeft = leftHeight(root);
        int hRight = rightHeight(root);
        if (hLeft == hRight) return pow(, hLeft) - ;
        return countNodes(root->left) + countNodes(root->right) + ;
    }
    int leftHeight(TreeNode* root) {
        if (!root) return ;
        return  + leftHeight(root->left);
    }
    int rightHeight(TreeNode* root) {
        if (!root) return ;
        return  + rightHeight(root->right);
    }
};

这道题还有一个标签是 Binary Search，但是在论坛上看了一圈下来，并没有发现有经典的二分搜索的写法，只找到了下面这个类似二分搜索的解法，感觉应该不算严格意义上的二分搜素法吧，毕竟 left，right 变量和 while 循环都没有，只是隐约有点二分搜索法的影子在里面，即根据条件选左右分区。首先我们需要一个 getHeight 函数，这是用来统计当前结点的左子树的最大高度的，因为一直走的是左子结点，若当前结点不存在，则返回 -1。我们对当前结点调用 getHeight 函数，得到左子树的最大高度h，若为 -1，则说明当前结点不存在，直接返回0。否则就对右子结点调用 getHeight 函数，若返回值为 h-1，说明左子树是一棵完美二叉树，则左子树的结点个数是 2^h-1 个，再加上当前结点，总共是 2^h 个，即 1<<h，此时再加上对右子结点调用递归函数的返回值即可。若对右子结点调用 getHeight 函数的返回值不为 h-1，说明右子树一定是完美树，且高度为 h-1，则总结点个数为 2^(h-1)-1，加上当前结点为 2^(h-1)，即 1<<(h-1)，然后再加上对左子结点调用递归函数的返回值即可。这样貌似也算一种二分搜索法吧，参见代码如下：

解法四：

class Solution {
public:
    int countNodes(TreeNode* root) {
        int res = , h = getHeight(root);
        if (h < ) return ;
        if (getHeight(root->right) == h - ) return ( << h) + countNodes(root->right);
        return ( << (h - )) + countNodes(root->left);
    }
    int getHeight(TreeNode* node) {
        return node ? ( + getHeight(node->left)) : -;
    }
};

我们也可以写成迭代的形式，用一个 while 循环，感觉好处是调用 getHeight 函数的次数变少了，因为开头计算的高度h可以一直用，每下一层后，h自减1即可，参见代码如下：

解法五：

class Solution {
public:
    int countNodes(TreeNode* root) {
        int res = , h = getHeight(root);
        if (h < ) return ;
        while (root) {
            if (getHeight(root->right) == h - ) {
                res +=  << h;
                root = root->right;
            } else {
                res +=  << (h - );
                root = root->left;
            }
            --h;
        }
        return res;
    }
    int getHeight(TreeNode* node) {
        return node ? ( + getHeight(node->left)) : -;
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/222

类似题目：

Closest Binary Search Tree Value

参考资料：

https://leetcode.com/problems/count-complete-tree-nodes/

https://leetcode.com/problems/count-complete-tree-nodes/discuss/61958/Concise-Java-solutions-O(log(n)2)

https://leetcode.com/problems/count-complete-tree-nodes/discuss/61953/Easy-short-c%2B%2B-recursive-solution

https://leetcode.com/problems/count-complete-tree-nodes/discuss/61948/Accepted-Easy-Understand-Java-Solution

LeetCode All in One 题目讲解汇总(持续更新中...)