poj3876 darts

Darts

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 58		Accepted: 32		Special Judge

Description

After a long week of work at the ICPC Headquarters, Bill and his friends usually go to a small pub on Friday evenings to have a couple of beers and play darts. All of them are well aware of the fact that their ability at darts decreases at the same rate as the amount of beer left in their mugs. 
They always play 501, one of the easiest games. Players start with a score of N points (typically, N = 501, hence the name) and take turns throwing darts. The score of each player decreases by the value of the section hit by the dart, unless the score becomes negative, in which case it remains unchanged. The first player to reach a score of 0 wins. The figure below shows the dartboard with which the game is played.

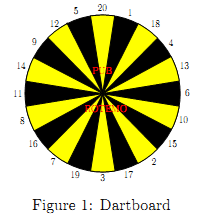
As the clock ticks closer to midnight and they start running out of beer, everyone wonders the same: is it worth trying to aim the dart at a specic section? Or is it better just to throw the dart at a random section on the dartboard? You are asked to deal with the question by finding out what would happen if two players (A and B) applying these two different strategies were to play against each other:

Player A throws the darts at random, and consequently they land with equal probability in each of the sections of the dartboard. 
If Player B aims at a certain section, the dart has the same probability of landing in the correct one as in each of the two adjacent ones (the neighbouring regions to the left and right). Moreover, he is completely aware of his ability and sober enough to aim at the section that maximizes his probability of winning.

Given the initial score of both players, can you determine the probability that the first player wins? Of course, being the first to throw a dart might be advantageous, so the answer depends on who plays first.

Input

The input consists of a series of lines, each containing an integer N (1 <= N <= 501), the initial score of both players. A case with N = 0 marks the end of the input and must not be processed.

Output

For each number in the input, your program should output a line containing two real numbers: the probability that A wins if A throws the first dart, and the probability that B wins if B throws the first dart. Your answers should be accurate to within an absolute or relative error of 10^-8.

Sample Input

5
100
0

Sample Output

0.136363636364 0.909090909091
0.072504908290 0.950215081962

题目大意：A，B两人比赛射飞镖，每个人都有一个一样的初始分数n，两人轮流扔。投中a时，如果n大于等于a，n=n-a，否则n不变。n先为0的一方胜。
         两人的策略不同，A随机射，每个数字射中的概率为20分之一。B瞄准某个数字射，但射中的概率只有三分之一，还有另外三分之一射中左右两个。
         给出N，求A先射A赢的概率以及B先射B赢的概率。
思路：很容易想出来是概率dp，特殊情况也比较比较好处理。但问题是这里的状态会出现从自身到自身的状态，即dp[i][j]的某一部分是由dp[i][j]推倒而来的，这就形成了一个环。这里有两种解决方法，一是将可能出现环的状态反复迭代做，做上几十次，这样将逐步逼近正确值。比较好写，但运行时间较长。二是把所有环列出，这样将会有许多个等式，然后用高斯消元直接求，速度比较快，但比较难写。
     本人采用的是第一种方法，但在poj上不是tle就是wa，实在找不出一个合适的迭代次数，无奈打表。下面给出打表程序。

 /*
  * Author:  Joshua
  * Created Time:  2014年08月23日 星期六 22时20分08秒
  * File Name: poj3876.cpp
  */
 #include<cstdio>
 #define maxn 505
 int a[]={,,,,,,,,,,,,,,,,,,,,,};
 double dp1[maxn][maxn],dp2[maxn][maxn];
 void solve()
 {
     for (int i=;i<maxn;++i)
     {
         dp1[][i]=;
         dp2[i][]=;
     }
     for (int i=;i<=;++i)
         for (int j=;j<=;++j)
         {
             for (int t=;t<=;++t)
             {
                 dp1[i][j]=;
                 for (int k=;k<;++k)
                     if (i-a[k]>=)
                         dp1[i][j]+=(-dp2[i-a[k]][j])/20.0;
                     else
                         dp1[i][j]+=(-dp2[i][j])/20.0;
                 dp2[i][j]=;
                 for (int k=;k<;++k)
                 {
                     double temp=;
                     for (int l=;l<=;++l)
                         if (j-a[k+l]>=)
                             temp+=(-dp1[i][j-a[k+l]])/3.0;
                         else
                             temp+=(-dp1[i][j])/3.0;
                     if (temp>dp2[i][j]) dp2[i][j]=temp;
                 }
                 if (i> && j>) break;
             }
         }
 }
 int main()
 {
     int n;
     solve();
     while (scanf("%d",&n) && n)
     {
         printf("%.12f %.12f\n",dp1[n][n],dp2[n][n]);
     }

     return ;
 }