已知前序（后序）遍历序列和中序遍历序列构建二叉树（Leetcode相关题目）

1.文字描述：

已知一颗二叉树的前序（后序）遍历序列和中序遍历序列，如何构建这棵二叉树？

以前序为例子：

前序遍历序列：ABCDEF

中序遍历序列：CBDAEF

前序遍历先访问根节点，因此前序遍历序列的第一个字母肯定就是根节点，即A是根节点；然后，由于中序遍历先访问左子树，再访问根节点，最后访问右子树，所以我们找到中序遍历中A的位置，然后A左边的字母就是左子树了，也就是CBD是根节点的左子树；同样的，得到EF为根节点的右子树。

将前序遍历序列分成BCD和EF，分别对左子树和右子树应用同样的方法，递归下去，二叉树就成功构建好了。如下图：

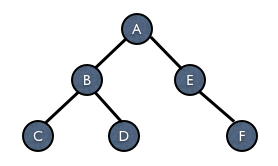
假如已知的是中序和后序遍历的序列，原理也一样。由于后序是先访问左子树，然后访问右子树，最后访问根节点，因此我们确定后序遍历序列的最后一个字母为根节点。其他步骤一样，用中序遍历序列找出两棵子树，再进行同样的操作。

2.代码实现：

（1）已知前序和中序：

Leetcode题目：

105 Construct Binary Tree from Preorder and Inorder Traversal（https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/）

代码：

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildTree(preorder, inorder, , preorder.size() - , , inorder.size() - );
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder, int preStart, int preEnd, int inStart, int inEnd) {
        if (preStart > preEnd || inStart > inEnd) return NULL;
        TreeNode *res;
        res = new TreeNode(preorder[preStart]);
        int flag;
        for (int i = inStart; i <= inEnd; i++) {
            if (preorder[preStart] == inorder[i]) {
                flag = i;
                break;
            }
        }
        res->left = buildTree(preorder, inorder, preStart + , preStart + flag - inStart, inStart, flag - );
        res->right = buildTree(preorder, inorder, preStart + flag - inStart + , preEnd, flag + , inEnd);
        return res;
    }
};

一开始我采用的做法是遇到的每棵子树都用新的vector数组来存放它的中序和前序遍历序列，但这样又浪费空间又增加时间，我们只要用原来的vector数组就可以了。

因此我们要用preStart，preEnd，inStart和inEnd来保存序列开始和结束的位置。比较容易得出的是inStart和inEnd这两个位置；难理解的是左子树的preEnd和右子树的preStart。但是我们求出左子树的preEnd后，只要加1就是右子树的preStart了。而要求左子树的preEnd我们可以通过中序来求出左子树的元素个数，然后就可以求出这个位置了。

（1）已知中序和后序：

Leetcode题目：

106 Construct Binary Tree from Inorder and Postorder Traversal（https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/）

代码：

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return buildTree(inorder, postorder, , inorder.size() - , postorder.size() - , );
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder, int inStart, int inEnd, int postEnd, int postStart) {
        if (inStart > inEnd || postEnd < postStart) {
            return NULL;
        }
        int flag;
        TreeNode *res = new TreeNode(postorder[postEnd]);
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == postorder[postEnd]) {
                flag = i;
                break;
            }
        }
        res->left = buildTree(inorder, postorder, inStart, flag - , postStart - inStart + flag - , postStart);
        res->right = buildTree(inorder, postorder, flag + , inEnd, postEnd - , postEnd - inEnd + flag);
        return res;
    }
};