NP完整性| 集1（简介）

我们一直在写关于高效算法来解决复杂问题，如最短路径，欧拉图，最小生成树等。这些都是算法设计者的成功故事。 在这篇文章中，讨论了计算机科学的失败故事。

计算机可以解决所有的计算问题吗？

存在计算问题，即使在无限制的时间内，算法也无法解决。例如图灵暂停（Turing Halting）问题（给定一个程序和一个输入，程序是否会在使用该输入运行时终止，否则将永远运行）。Alan Turing证明，解决所有可能的程序输入对的停止问题的一般算法不可能存在。证明的关键部分是，图灵机被用作计算机和程序的数学定义（源停止问题）。

NP完全问题是另一个失败的故事，NP完全问题是问题的状态是未知的。对于任何NP完全问题，还没有发现多项式时间算法内可以解决，也没有任何人能够证明任何一个都不存在多项式时间算法。有趣的是，如果在多项式时间内可以解决NP完全问题中的任何一个，那么所有这些都可以解决。

什么是NP，P，NP完成和NP-Hard问题？（提示：昨天我写过一篇文章里面有介绍）
P问题是一系列可以在多项式时间内在确定的机器上可以被解决的问题。

NP问题是一系列的可以由一个在多项式时间内在非确定性图灵机实现的问题。P是NP的子集（多项式时间中可以通过确定性机器求解的任何问题也可以在多项式时间内由非确定性机器求解）。

非正式地，NP是通过“幸运算法”的多项式时间解决的决策问题集合，这是一种在给定的选择集合（Source Ref 1）中始终作出正确猜测的神奇算法。

NP完整的问题是NP集中最难的问题。

一个决策问题是一个NP完全问题，当且仅当下面条件成立：
1） L在NP中（NP的完整问题的任何给定解决方案可以快速验证，但没有有效的已知解决方案），则决策问题L为NP完成。
2） NP中的每个问题在多项式时间内可以减少为L（减少定义如下）。

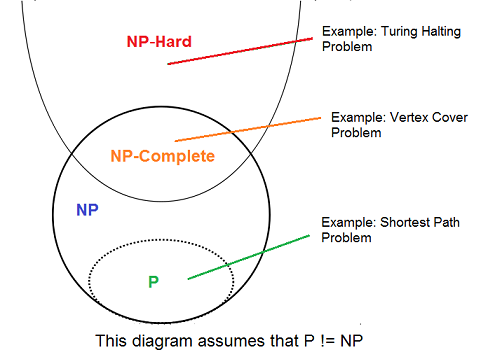
一个问题是NP-Hard如果遵循上述属性2，不需要遵循属性1.因此，NP-Complete问题也是NP-Hard问题的一个子集。

决策与优化问题
NP完整性适用于决策问题的领域。这样做是因为比较优化问题的决策问题的难度比较容易。实际上，尽管在多项式时间内能够解决决策问题通常也可以使我们在多项式时间内解决相应的优化问题（使用多项式调用决策问题）。因此，讨论决策问题的难度通常与讨论优化问题的难度相当。（来源参考文献2）。
例如，考虑顶点覆盖问题（给定一个图形，找出覆盖所有边缘的最小尺寸顶点集）。这是一个优化问题。相应的决策问题是，给定无向图G和k，是否存在大小为k的顶点覆盖？

什么是约简？
令 L₁和L₂是两个决策问题。假设算法A₂求解L₂。也就是说，如果y是L₂的一个输入，则算法A₂将输出是，不根据是否属于L₂来回答是或否。
该思想是找到从L₁到L₂的变换，使得算法A₂可以是算法A₁的一部分，从而求解L₁。

学习约简是非常重要的。例如，如果我们有库函数来解决某些问题，如果我们可以将一个新的问题归纳到一个解决的问题，我们节省了大量的时间。考虑一个问题的例子，我们必须在给定的有向图中找到最小产品路径，其中路径的乘积是沿着路径的边的权重的乘积。如果我们有Dijkstra算法的代码找到最短路径，我们可以采用所有权重的记录，并使用Dijkstra的算法找到最小的产品路径，而不是为这个新问题写一个新的代码。

如何证明给定的问题是NP完成？
从NP-complete问题的定义看，似乎不可能证明问题L是NP-Complete。根据定义，它要求我们显示NP中的每个问题都是多项式时间可以约简到L.幸运的是，有一种替代方法来证明它。这个想法是采取已知的NP-Complete问题并将其减少到L.如果可以进行多项式时间减少，我们可以证明L是通过减少传递性的NP-Complete（如果在多项式中可以将NP完全问题简化为L时间，则所有问题都可以在多项式时间内缩减为L）。

NP-Complete的第一个问题是什么？
NP-Complete问题的定义必然会出现一些第一个NP-Complete问题。  SAT（布尔可满足性问题）是Cook证明的第一个NP-Complete问题（见CLRS书的证明）。

了解NP-Completeness甚至对于工程师来说总是有用的。假设您被要求编写一个有效的算法来解决贵公司极其重要的问题。经过很长时间的思考，你只能拿出指数时间的方法，这是不切实际的。如果您不了解NP完整性，您只能说我无法使用高效的算法。如果您了解NP完整性，并证明问题为NP完成，您可以自豪地说多项式时间解决方案不太可能存在。如果有多项式时间解可行，那么该解决方案解决了许多科学家多年来一直在努力的计算机科学的一个大问题。

我们很快将讨论更多的NP-Complete问题及其对NP完整性的证明。