java递归的应用和实例

使用计算机计算组合数：

1.使用组合数公式利用n!来计算

设计思想

（1）首先解决求n!的函数

（2）再结合组合数公式，求组合数

程序流程图

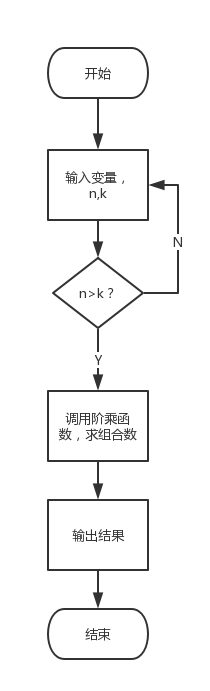
源程序代码

package Zuote;

import java.math.BigInteger;

import java.util.Scanner;

public class Zuoye1 {

public static void main(String args[])

{

       Scanner input=new Scanner(System.in);

       int n,k;//组合数公式中的n k

       System.out.println("请输入组合数公式的n和k：");

       n=input.nextInt();

       k=input.nextInt();

       while(k>=n)//判断输入是否符合公式，不符合提示错误，重新输入

       {

              System.out.println("输入错误，请重新输入");

              System.out.println("请输入组合数公式的n和k：");

              n=input.nextInt();

              k=input.nextInt();

       }

       long C;

       C=calculateN(n)/(calculateN(k)*calculateN(n-k));

       System.out.println("结果为"+C);

}

public static long calculateN(int n)//计算n!的递归公式

{

       if(n==1 || n==0){

              return 1;

       }

      

       return n*calculateN(n-1);

}

}

结果截图

2.使用递推的方法用杨辉三角形计算

设计思想

（1）     构建杨辉三角

（2）     组合数结果就相当于杨辉三角中的一个数，n为行，k为列

（3）     输出相应的数就可以

程序流程图

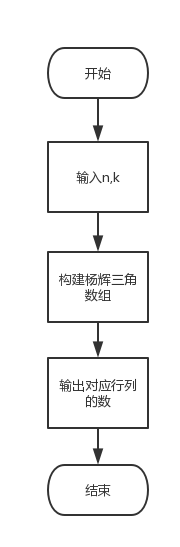
源程序代码

package Zuote;

import java.util.Scanner;

public class Zuoye2 {

public static void main(String args[])

{

Scanner input=new Scanner(System.in);

int n,k;//组合数公式中的n k

System.out.println("请输入组合数公式的n和k：");

n=input.nextInt();

k=input.nextInt();

int [][]f=new int[27][27];//构建杨辉三角

f[0][0] = 1;

for(int i = 1;i <= 24;i++)

{

for(int j = 1;j <= i + 1;j++)

{

f[i][j] = f[i - 1][j - 1] + f[i - 1][j];

}

}

System.out.println("组合结果为"+f[n+1][k+1]);//输出结果

}

}

结果截图

3. 使用递归的方法用组合数递推公式计算

设计思想

（1）    递归组合数，相当于杨辉三角

（2）     构建递归函数，n,k相应于杨辉三角的行列

程序流程图

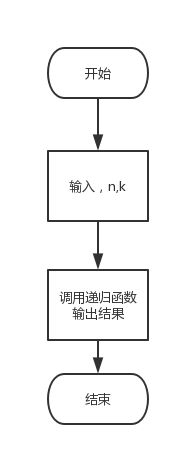
源程序代码

package Zuote;

import java.util.Scanner;

public class Zuoye3 {

public static void main(String args[])

{

Scanner input=new Scanner(System.in);

int n,k;//组合数公式中的n k

System.out.println("请输入组合数公式的n和k：");

n=input.nextInt();

k=input.nextInt();

System.out.println("组合结果为"+ZuHe(n,k));

}

public static long ZuHe(int a,int b) //构造递归函数

{

if(b==0)return 1;

else {

if(a==1)return 1;

else {

if(a==b)return 1;

else {

return (ZuHe(a-1,b-1)+ZuHe(a-1,b));

}

}

}

}

}

结果截图

4.递归编程解决汉诺塔问题。用Java实现

设计思想

（1）    递归移动n个圆盘，先移动n-1个，再把第n个移动到c上

（2）    递归，依次移动

程序流程图

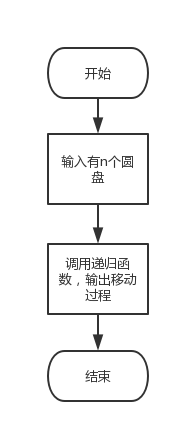
源程序代码

package Zuote;

import java.util.Scanner;

public class Zuoye4 {

public static void main(String args[])

{

int n;//有n个圆盘

char A='A';

char B='B';

char C='C';

Scanner input=new Scanner(System.in);

System.out.println("请输入n：");

n=input.nextInt();

Hanoi( n,A,B,C);

}

public static void Hanoi(int n,char A,char B,char C)//将 n个圆盘从A移动到C，B做辅助

{

if(n==1)

{

move(A,1,C);

}

else

{

Hanoi(n-1,A,C,B);

move(A,n,C);

Hanoi(n-1,B,A,C);

}

}

public static void move(char A,int n,char B)//将第n个圆盘从A移动到B

{

System.out.println("第"+n+"个圆盘从"+A+"->"+B);

}

}

结果截图

5.使用递归方式判断某个字串是否是回文

设计思想

（1）    从开头开始依次比较首尾字符

（2）    如果相同，再比较第二个字符和倒数第二个

（3）    依次比较直到最后完全相同，输出

程序流程图

源程序代码

package Zuote;

import java.util.Scanner;

public class Zuoye5 {

public static void main(String args[])

{

Scanner input=new Scanner(System.in);

String s=input.next();//输入字符串

int i,j;

i=0;//为字符串第一个字符

j=s.length()-1;//最后一个字符

System.out.println("是否是回文:"+HuiWen(s,i,j));

}

public static boolean HuiWen(String s,int i,int j)//判断字符串是否回文

{

if(i==j)

{

return true;

}

else

if((i-1)==j)

{

return true;

}

return (s.charAt(i)==s.charAt(j))&&HuiWen(s,i+1,j-1);

}

}

结果截图