常见的排序算法总结（JavaScript）

引言

　　排序算法是数据结构和算法之中的基本功，无论是在笔试还是面试，还是实际运用中都有着很基础的地位。这不正直七月，每年校招的备战期，所以想把常见的排序算法记录下来。在本篇文章中的排序算法使用 JavaScript 实现。

一、 冒泡排序

　　冒泡排序是排序算法中最简单的一个算法，其优点是易理解，易实现。在一些对性能要求不高且数据量不大的需求中，冒泡排序是一个很好的选择。

　　原理：假设排序顺序为增序，数组长度为 N。数组每相邻两个元素进行比较，大数后移，小数前移，第一轮排序下来就能找到最大的数。也就是比较 A[i] 和 A[i+1] ，将大数后移，随后增加 i 的值，再进行比较。第二轮再对剩余的 N-1 个数进行排序，找出第二大的数，以此类推。同时也可以记录交换次数来进行优化，如果在一层循环之中交换次数为 0，则排序结束。

　　下面这张图展示了冒泡排序的全过程：

　　下面这张图展示冒泡排序在宏观层面的全过程：

　　

平均时间复杂度	最优时间负复杂度	最坏时间复杂度	空间复杂度
O(n^2)	O(n)	O(n^2)	O(1)

　　

 function bubbleSort (arr) {
     var swapTime = 0;
     for(var i = 0, length1 = arr.length; i < length1; i ++){
         for(var j = 0, length2 = length1 - i; j < length2 - 1; j ++){
             if(arr[j] > arr[j+1]){
                 swapTime++;
                 var temp = arr[j];
                 arr[j] = arr[j+1];
                 arr[j+1] = temp;
             }
         }
         //检查交换次数，如果为0，则当前数组为有序数组；如不为0，则重置
         if(swapTime === 0){
             break;
         }else {
             swapTime = 0;
         }
     }
 }

二、选择排序

　　选择排序算法与冒泡排序算法类似，即每一轮找出一个最大值。但和冒泡排序不同的一点是，冒泡排序是采用不停的交换将最大值（最小值）筛选出来，而选择排序是记录下最大值（最小值）的索引。

　　原理：假设排序方式为增序，数组长度为 N。设置最大值索引初始值 index = 0，然后遍历数组，记录下最大值的索引，即比较 A[i] 与 A[index] 的值，若 A[i] > A[index] 则更新 index = i。在每一轮遍历结束后，交换 index 位置和末尾位置的值，即交换 A[index] 和 A[i]，这样便保证了末尾值是最大值。随后对剩余的 N-1 个数进行同样的方式排序，以此类推。　　

　　下面这张图展示了选择排序的全过程：

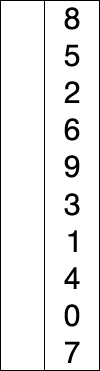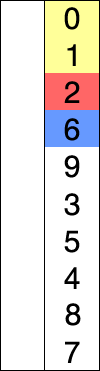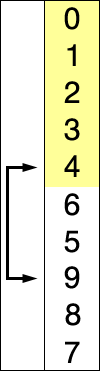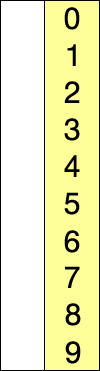
　　下面这张图展示了在宏观层面上选择排序的全过程：

平均时间复杂度	最优时间复杂度	最差时间复杂度	空间复杂度
O(n^2)	O(n^2)	O(n^2)	O(1)

 function selectSort (arr) {
     for(var i = 0, length1 = arr.length; i < length1; i ++){
         var index = 0
         for(var j = 0, length2 = length1 - i; j < length2; j ++){
             if(arr[j] > arr[index]){
                 index = j;
             }
         }
         var temp = arr[index];
         arr[index] = arr[length1 - i - 1];
         arr[length1 - i - 1] = temp;
     }
 }

三、插入排序

　　插入排序的思想是将原始数组划分成两侧，一侧是有序数组，一侧是无序数组。每次取出无序数组的一个元素，将它插入到有序数组的正确位置上，这种方式也会导致有序数组中其插入位置之后的元素全部后移。插入排序的思想类似于我们抓扑克牌。

　　原理：假设排序方式为增序，数组长度为 N。初始设 A[0] 为有序数组，A[1] ~ A[N-1] 为无序数组，取出 A[1] 将其插入至有序数组中的正确位置，使得有序数组增大为 A[0] ~ A[1]。继续取 A[2] 将其插入至有序表数组的正确位置，以此类推，直至无序数组取完。

　　下面这张图展示了插入排序的全过程：

　　下面这张图展示了在宏观层面上插入排序的全过程：

平均时间复杂度	最优时间复杂度	最差时间复杂度	空间复杂度
O(n^2)	O(n^2)	O(n^2)	O(1)

 function insertSort (arr) {
     for(var i = 0, length1 = arr.length; i < length1; i ++){
         for(var j = 0, length2 = i + 1; j < length2; j ++){
             if(arr[j] > arr[length2]){
                 var temp = arr[length2];
                 for(var k = length2; k > j; k --){
                     arr[k] = arr[k-1];
                 }
                 arr[j] = temp;
             }
         }
     }
 }

四、 希尔排序

　　希尔排序是优化过后的插入，其算法的思想是在插入排序的基础上加上了一个步长 gap，通过步长将数组分成若干个子项，先分别对子项进行插入排序，使得每一个元素朝着最终目的地跨了一大步。然后逐步缩小步长，这种排序算法也是不稳定的。

　　原理：假设排序方式为增序，数组长度为 N。首先取步长 gap = N/2，那么便将 N 长度的数组拆分成了 [A[0], A[gap]]，[A[1], A[gap+1]]，[A[2], A[gap+3]] ... ... [A[gap-1], A[N-1]] 子数组，分别对子数组进行插入排序。随后逐步缩小步长，再进行插入排序，直至步长为 1。

　　下面这张图展示了希尔排序的全过程：

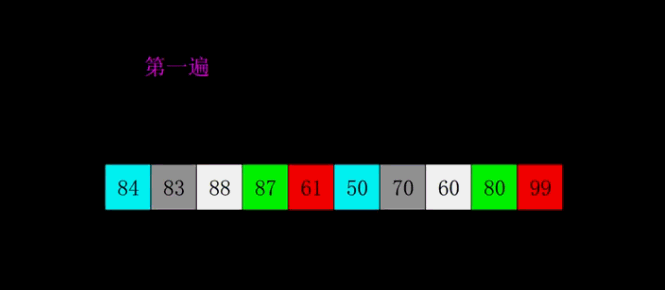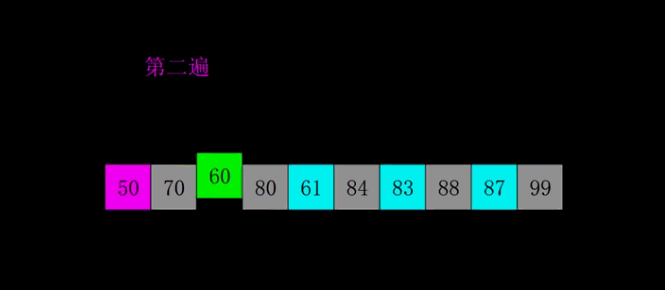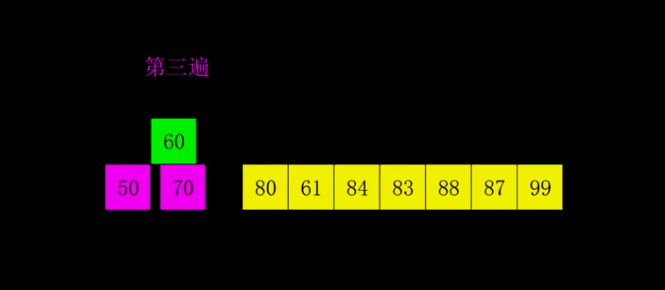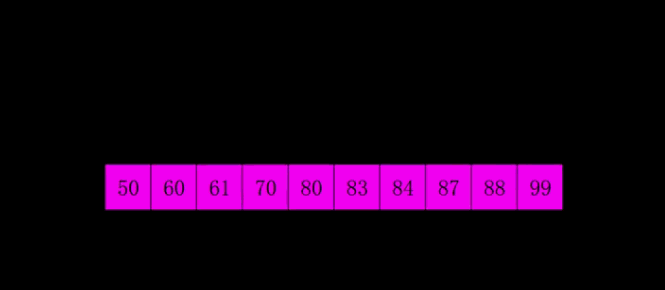
　　下面这张图展示了希尔排序在宏观上的全过程：

平均时间复杂度	最优时间复杂度	最差时间复杂度	空间复杂度
O(nLogn)~O(n^2)	O(n^1.3)	O(n^2)	O(1)

 function shellSort(arr) {
     var gap = Math.floor(arr.length / 2);
     while (gap >= 1) {
         for (var i = 0; i < gap; i++) {
             for (var j = i; j < arr.length; j += gap) {
                 for (var k = i, length = j + gap; k < length; k += gap) {
                     if (arr[k] > arr[length]) {
                         var temp = arr[length];
                         for (var x = length; x > k; x = x - gap) {
                             arr[x] = arr[x - gap];
                         }
                         arr[k] = temp;
                     }
                 }
             }
         }
         gap = Math.floor(gap / 2);
     }
 }

五、归并排序 　　

　　归并排序是分治法思想的典型应用，我们可以把一个 N 规模的问题分解成若干个小规模的子问题，用子问题的解来求解原问题。这同时也涉及到了问题的求解顺序，在动态规划算法中有自顶向下和自底向上两种不同的求解顺序。在这里一般采用的是自底向上的求解方法，比如一个 N 长度的数组，我们可以分解成 N/2 个长度为 2 或 1 的子数组，分别对子数组排序，再进行两两相并，直到归并成原始数组。

　　原理：假设排序顺序为增序，数组长度为 N。将数组拆分成 N 个长度为 1 的数组。然后相邻子数组进行归并，形成若干个长度为 2 或者 1 的数组，再继续进行归并，直至长度为 N。　

　　下面这张图展示了归并的排序的全过程：　

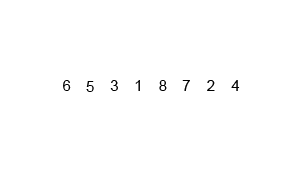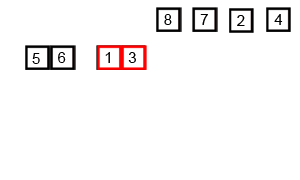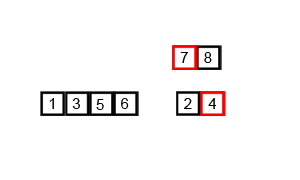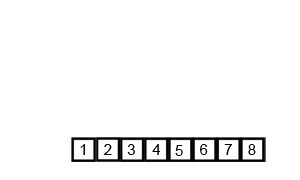
　　下面这张图展示了在宏观层面上归并排序的全过程：

平均时间复杂度	最优时间复杂度	最差时间复杂度	空间复杂度
O(nLogn)	O(nLogn)	O(nLogn)	O(n)

 function mergeSort(arr) {
     var n = 1;
     while (n < arr.length) {
         for (var i = 0; i < arr.length; i += n*2) {
             var arr1 = arr.slice(i, i+n);
             var arr2 = arr.slice(i+n, i+(n*2));
             var temp = [];
             while(arr1.length != 0 || arr2.length != 0){
                 if(arr1.length === 0){
                     temp.push(arr2.shift());
                     continue;
                 }
                 if(arr2.length === 0){
                     temp.push(arr1.shift());
                     continue;
                 }
                 if(arr1[0] < arr2[0]){
                     temp.push(arr1.shift());
                 }else{
                     temp.push(arr2.shift());
                 }
             }
             arr.splice(i, n*2, ...temp);
         }
         n = n * 2;
     }
 }

六、快速排序

　　快速排序同样也使用了分治法的思想，在实际运用中使用的最多的就是快速排序。快速排序的核心思想是运用递归法，在每轮排序时指定一个基数，将基数移动到正确的位置上，然后再把基数的左右两边拆分出来，并分别进行相同的排序处理，直到其子数组长度为 1。其采用的是自顶向下的处理法。

　　原理：在每一轮排序中取一个基数 k ， 设 i 和 j 分别为数组的最左端和最右端，i 坐标从起始点向 k 点遍历，若找到一个比 k 大的元素，则停下来等待 j 的遍历。 j 坐标从起始点向 k 点遍历，若找到一个比 k 小的元素，则 i 和 j 坐标的元素互相交换。若有一端提前到达了 k 点，则等待满足条件后与另一端坐标交换。当 i 和 j 碰撞时，则为分治点，此时 i 和 j 相碰撞的坐标元素便是它的最终位置，以碰撞点为中心将数组拆分成两段，并进行相同的递归处理。当 i >= j 时，则为回退点。

　　下面给出一张维基百科上的图，展示了一轮快速排序的过程：

　

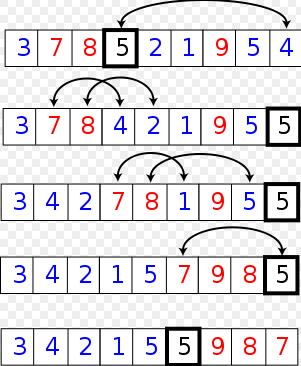
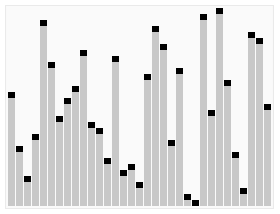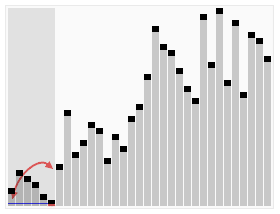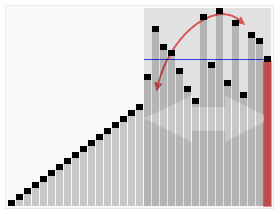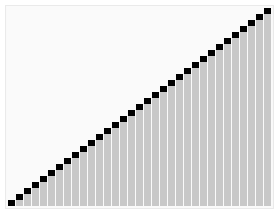
　　下面这张图展示了一段快速排序的全过程：

　　

平均时间复杂度	最优时间复杂度	最差时间复杂度	空间复杂度
O(nLogn)	O(nLogn)	O(n^2)	O(1)

 function quickSort (arr) {
     function sort(array, first, last) {
         if (first >= last) {
             return;
         }
         var base = Math.floor((first + last) / 2);
         var i = first - 1;
         var j = last - 1;
         var temp;
         while (j > i) {
             while (j > i && array[j] > array[base]) {
                 j--;
             }
             while (i < j && array[i] <= array[base]) {
                 i++;
             }
             temp = array[i];
             array[i] = array[j];
             array[j] = temp;
         }
         temp = array[base];
         array[base] = array[i];
         array[i] = temp;
         sort(array, first, i);
         sort(array, i + 2, last)
     }
     sort(arr, 1, arr.length);
 }

　　在这里我们 JavaScript 描绘出快速排序的过程：