zkw线段树--非递归线段树

　　为什么要学习非递归线段树，这个问题大部分博客解释为普通线段树常数大，会被卡常，即虽然都是O(logn)，其实在一些具有可加性的问题中树状数组一般跑的比线段树快。于我个人而言，原因有二：一是我冥冥之中有一种感觉，线段树和树状数组本质上没有什么区别（这个就比较玄学）;二是受FFT中位逆序置换启发（但是还没有学会FFT），线段树也是一种分治，甚至是很完美的那种，从递归到非递归毫无疑问是一种优化方案。所以当我看到zkw学长的线段树讲义，他里面提到线段树可以是树状数组，平衡树等我颇感兴趣（三十六方，必为大统）

　　话不多说，我们直接开始学习（建议先把握普通线段树再学，可能大部分题目不是必须要非递归，但是可以加深理解，而且一些处理挺有意思的）

　　按照常用模板来讲解

　　一：单点修改，区间查询

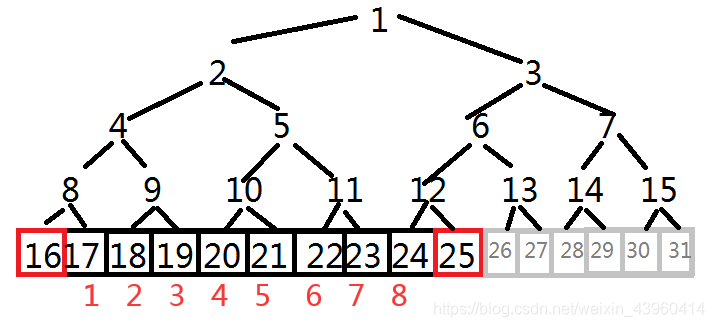　　（这是我认为最好的图解，请按我的解释仔细体味，后面本人没准备图，全靠在这上面脑测）

　　如图，这是一个在维护一个长度为8的数组,采用的是堆式存储的方法,故维护线段树的数组要开4N(N为原数组长度),与普通的线段树不同的是他不是从第一片叶子开始存储的，而是在第二片，与之对应的是图上2个红方框的元素，我们称其为哨兵，为什么要这2个哨兵呢？这是为了实现区间查询，后文解释

　　建树:

　　上图我们知道叶子数为N + 2（含哨兵）,但是我们是要将它补为完全二叉树（有很多优秀性质）来实现迭代更新操作,所以实际叶子数应该是大于等于N + 2的最小的2的整数次幂，记为bit，则根据二叉树的性质，非叶子节点数有bit - 1个，由于第一片叶子是哨兵（数组下标为bit），所以我们直接从bit + 1开始存（是不是很好的性质啊），先求下bit：

　　for(bit = 1; bit < n + 2; bit <<= 1);　　代码中n为数组大小，然后bit和后续操作息息相关，我们设为全局变量

　　存储叶子节点:　　for(int i = 1; i <= n; i++) dat[bit + i] = a[i];　　a数组即为原数组

　　然后直接向上传递即可：

　　for(int i = bit - 1; i; i--)　　dat[i] = dat[i << 1] + dat[i << 1 | 1];

void build(int n){
    　　for(bit = 1; bit < n + 2; bit <<= 1);
    　　for(int i = 1; i <= n; i++) dat[bit + i] = read();//这是个快读，因为一些题中原数组用处不大，看个人习惯吧，因人和题目而异
    　　for(int i = bit - 1; i; i--)    dat[i] = dat[lc(i)] + dat[rc(i)];
　　}

　　那么就建完了，把握住逻辑甚至比递归还好写

　　单点修改：

　　单点修改也是很简单，因为我们根据堆式存储和bit已经可以刻画出线段树了，所以更新就是直接定位修改，然后向上传递

　　

void modify(int x, int v){
    　　for(dat[x += bit] += v, x >>= 1; x; x >>= 1) dat[x] = dat[lc(x)] + dat[rc(x)];//x 是元素在原数组的位置，结合前面的分析bit + x就是在线段树中的位置，后面不在提及。然后不断跳到父节点修改
　　}

 

　　这里实现的是单点增加和求区间和的操作，具体因题目而异

　　区间查询：

　　哨兵启动！线段树一个优势就是它把区间划分便于操作的同时能应对所有的问询，而在递归版中我们可以很自然的理解方法，放到迭代如何呢？zkw学长采用了一种很聪明的方法，利用包裹的方法，具体的我们结合代码分析（如果学过LCA会好理解一点个人感觉）

　　

int quiry(int l, int r){//不要吐槽我的命名啦
　　　　int ans = 0;
　　　　for(l += (bit - 1), r += (bit + 1); l ^ r ^ 1; l >>= 1, r >>= 1){//传入的参数中[l,r]是待查询区间，而我们定位到的(l, r)是一个包含代查询区间的最小开区间(左右即为哨兵)，原因？先接着看下去；l ^ r ^ 1,这是判断是否已经完全覆盖到了要查询的区间，即左右哨兵成为了兄弟（兄弟节点异或结果为1,再异或1为0退出）
　　　　　　if(~l & 1) ans += dat[l ^ 1];//如果左边的哨兵是左子树，因为最小包含的缘故，其右子树必然在区间内，累加入答案，不熟悉位运算的可能要理解下
　　　　　　if(r & 1) ans += dat[r ^ 1];//右哨兵同理
　　　　}
　　　　return ans;
　　}

　　结合图片实例体会：

　　假设我们要查询的就是[2,7],那么定位后的l = 17, r = 24,二者不符合累加条件，跳到父节点

　　我们发现r无论如何不能满足

　　l = 8,是左子树，故其右子树9包含的元素累加, r=12

　　l = 4,继续加节点5包含的元素, r = 6

　　l = 2, r = 3,变成兄弟了，退出

完整代码：　　

#include<iostream>
using namespace std;
int read(){
    int f = 1, x = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')   f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return f * x;
}
const int N = 5e5 + 3;
int dat[N * 2], bit;
#define lc(x) x << 1
#define rc(x) (x << 1) | 1
void build(int n){
    for(bit = 1; bit < n + 2; bit <<= 1);
    for(int i = 1; i <= n; i++) dat[bit + i] = read();
    for(int i = bit - 1; i; i--)    dat[i] = dat[lc(i)] + dat[rc(i)];
}
void modify(int x, int v){
    for(dat[x += bit] += v, x >>= 1; x; x >>= 1) dat[x] = dat[lc(x)] + dat[rc(x)];
}
int quiry(int l, int r){
    l = bit + l - 1, r = bit + r + 1;
    int ans = 0;
    while(l ^ r ^ 1){
        if(~l & 1)  ans += dat[l ^ 1];
        if(r & 1)   ans += dat[r ^ 1];
        l >>= 1;
        r >>= 1;
    }
    return ans;
}
signed main(){
    int n = read(), q = read();
    build(n);
    while(q--){
        int op = read(), x = read(), y = read();
        if(op == 1) modify(x, y);
        else    printf("%d\n",quiry(x, y));
    }
    return 0;
}

区间修改，区间查询（单点查询直接令查询区间是[x,x]就行）　　

struct seg{
 　　int dat, lzy;
 　　#define dat(x) tr[x].dat
 　　#define lzy(x) tr[x].lzy
　}tr[N << 2];
　#define lc(x) x << 1
　#define rc(x) (x << 1) | 1

　　先展示下定义　　

建树变化不大：

void build(int n){
 for(bit = 1; bit < n + 2; bit <<= 1);
 for(int i = 1; i <= n; i++) dat(bit + i) = read();
 for(int i = bit - 1; i; i--) dat(i) = dat(lc(i)) + dat(rc(i));
}

区间修改：

修改自下而上记录下左右哨兵包含的区间内有多少个元素被覆盖即可

void modify(int l, int r, int v){
 int llen = 0, rlen = 0, len = 1;//左右哨兵的被覆盖长度以及向上跳跃后节点区间变化
 for(l += (bit - 1), r += (bit + 1); l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1){
 if(~l & 1) lzy(l ^ 1) += v, llen += len;//标记永久化
 if(r & 1) lzy(r ^ 1) += v, rlen += len;
 dat(l >> 1) += v * llen, dat(r >> 1) += v * rlen; //如果l一直是右子树这llen为0,否则它的父节点的值应该加上左子树的区间增量，r同理
 }
 for(llen += rlen, l >>= 1; l; l >>= 1) dat(l) += v * llen;//当兄弟相遇直接一路传递到根就行
}

区间查询:

和上面差不多，加上lzy的增量即可

int quiry(int l, int r){
 int llen = 0, rlen = 0, len = 1, ans = 0;
 for(l += (bit - 1), r += (bit + 1); l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1){
 if(~l & 1) ans += dat(l ^ 1) + lzy(l ^ 1) * len, llen += len;
 if(r & 1) ans += dat(r ^ 1) + lzy(r ^ 1) * len, rlen += len;
 ans += lzy(l >> 1) * llen + lzy(r >> 1) * rlen;
 //if判断为真值的必然是全部包含在待查询区间的，因此直接乘len即可，而当llen和rlen不为0且哨兵的父节点带有懒标记时，答案应加上哨兵的兄弟被包含在区间里的长度
 }
 for(llen += rlen, l >>= 1; l; l >>= 1) ans += lzy(l) * llen;//因为标记是modify从哨兵一路上传，l，r之间的区间不会有标记，但是含lzy的区间一定是全部有增量，所以要一路上溯累加
 return ans;
}

完整代码在这里：

#include<iostream>
using namespace std;
#define int long long
int read(){
    int f = 1, x = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')   f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return f * x;
}
const int N = 1e6 + 3;
struct seg{
    int dat, lzy;
    #define dat(x) tr[x].dat
    #define lzy(x) tr[x].lzy
}tr[N << 2];
int bit;
#define lc(x) x << 1
#define rc(x) (x << 1) | 1
void build(int n){
    for(bit = 1; bit < n + 2; bit <<= 1);
    for(int i = 1; i <= n; i++) dat(bit + i) = read();
    for(int i = bit - 1; i; i--)    dat(i) = dat(lc(i)) + dat(rc(i));
}
void modify(int l, int r, int v){
    int llen = 0, rlen = 0, len = 1;
    for(l += (bit - 1), r += (bit + 1); l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1){
        if(~l & 1)  lzy(l ^ 1) += v, llen += len;
        if(r & 1)   lzy(r ^ 1) += v, rlen += len;
        dat(l >> 1) += v * llen, dat(r >> 1) += v * rlen;
    }
    for(llen += rlen,l >>= 1; l; l >>= 1)   dat(l) += v * llen;
}
int quiry(int l, int r){
    int llen = 0, rlen = 0, len = 1, ans = 0;
    for(l += (bit - 1), r += (bit + 1); l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1){
        if(~l & 1) ans += dat(l ^ 1) + lzy(l ^ 1) * len, llen += len;
        if(r & 1)   ans += dat(r ^ 1) + lzy(r ^ 1) * len, rlen += len;
        ans += lzy(l >> 1) * llen + lzy(r >> 1) * rlen;
    }
    for(llen += rlen, l >>= 1; l; l >>= 1)   ans += lzy(l) * llen;
    return ans;
}
signed main(){
    int n = read(), q = read();
    build(n);
    while(q--){
        int op = read();
        if(op == 1){
            int l = read(), r = read(), k = read();
            modify(l, r, k);
        }
        else{
            int x = read();
            printf("%lld\n",quiry(x, x));
        }
    }
    return 0;
}

根据某校OJ来看非递归区间加大概比递归快了3倍
总体而言，现在线段树在时间上优化有zkw线段树，空间上有动态开点
参考链接:（如有介意，联系我删除）
主要模板块学习

插图

原讲义