Delaunay Triangle 学习 2

参考

Delaunay Triangulation and Meshing Application to Finite Elements [book]

https://www.bilibili.com/video/BV1vi4y1x796?from=search&seid=8484114193065196500

https://en.wikipedia.org/wiki/Delaunay_triangulation 维基百科

http://paulbourke.net/papers/triangulate/ 所有带已经实现的代码

四面体的体积

\[V_{K}=\frac{1}{6}\left|\begin{array}{ccc}
x_{2}-x_{1} & x_{3}-x_{1} & x_{4}-x_{1} \\
y_{2}-y_{1} & y_{3}-y_{1} & y_{4}-y_{1} \\
z_{2}-z_{1} & z_{3}-z_{1} & z_{4}-z_{1}
\end{array}\right|
\]

面的点序

face 1: P4 P3 P2,
face 2: P1 P3 P4,
face 3: P4 P2 P1,
face 4: P1 P2 P3

边序列

edge 1：P1 P2,
edge 2：P1 P3,
edge 3：P1 P4,
edge 4：P2 P3,
edge 5：P2 P4,
edge 6：P3 P4,

求解四面体的球心的线性方程组

\[\Delta_{K}(x, y, z)=\left|\begin{array}{cccc}
l_{1}^{2}-l^{2} & l_{2}^{2}-l_{1}^{2} & l_{3}^{2}-l_{1}^{2} & l_{4}^{2}-l_{1}^{2} \\
x_{1}-x & x_{2}-x_{1} & x_{3}-x_{1} & x_{4}-x_{1} \\
y_{1}-y & y_{2}-y_{1} & y_{3}-y_{1} & y_{4}-y_{1} \\
z_{1}-z & z_{2}-z_{1} & z_{3}-z_{1} & z_{4}-z_{1}
\end{array}\right|
\]

其中$l^{2}=x^{2}+y^{2}+z^{2}$ 球心的坐标，即要求解的值。

直接求解四面体的外接圆的半径

$r_{k}=\frac{\sqrt{(a+b+c)(a+b-c)(b+c-a)(a-b+c)}}{24 V_{k}}$

其中a,b和c是四面体对应的边的乘积。

内切球的半径

\[\rho_{K}=\frac{3 V_{K}}{S_{1}+S_{2}+S_{3}+S_{4}}
\]

其中$S_i$ 是四面体的面的面积。

四面体的质量

\[Q_{K}=\alpha \frac{h_{\max }}{\rho_{K}}=\alpha \frac{h_{\max } S_{K}}{3 V_{K}}
\]

其中$S_K$表示四面体面的总面积$\alpha=\frac{\sqrt{6}}{12}$和从0-1描述质量的等式

\[Q_{K}=\beta \frac{h_{s}^{3}}{V_{K}}
\]

其中$h_{s}=\sqrt{\sum_{i=1}^{6} L_{i}^{2}}$和$L_i$表示四面体边的长度$\beta=\frac{\sqrt{3}}{216}$

重要提示

三维Delaunay元素允许条的存在。

三角化

欧拉公式

$ns - na + ne + c = 2$ 其中ns是顶点数量，na是边的数量，ne是元素的数量，c是连接的组件边界三角化的数量（2d）

$ns - na + nf - ne = cste$ 其中nf三角化面片的数量，cste是一个常量链接拓扑的区域

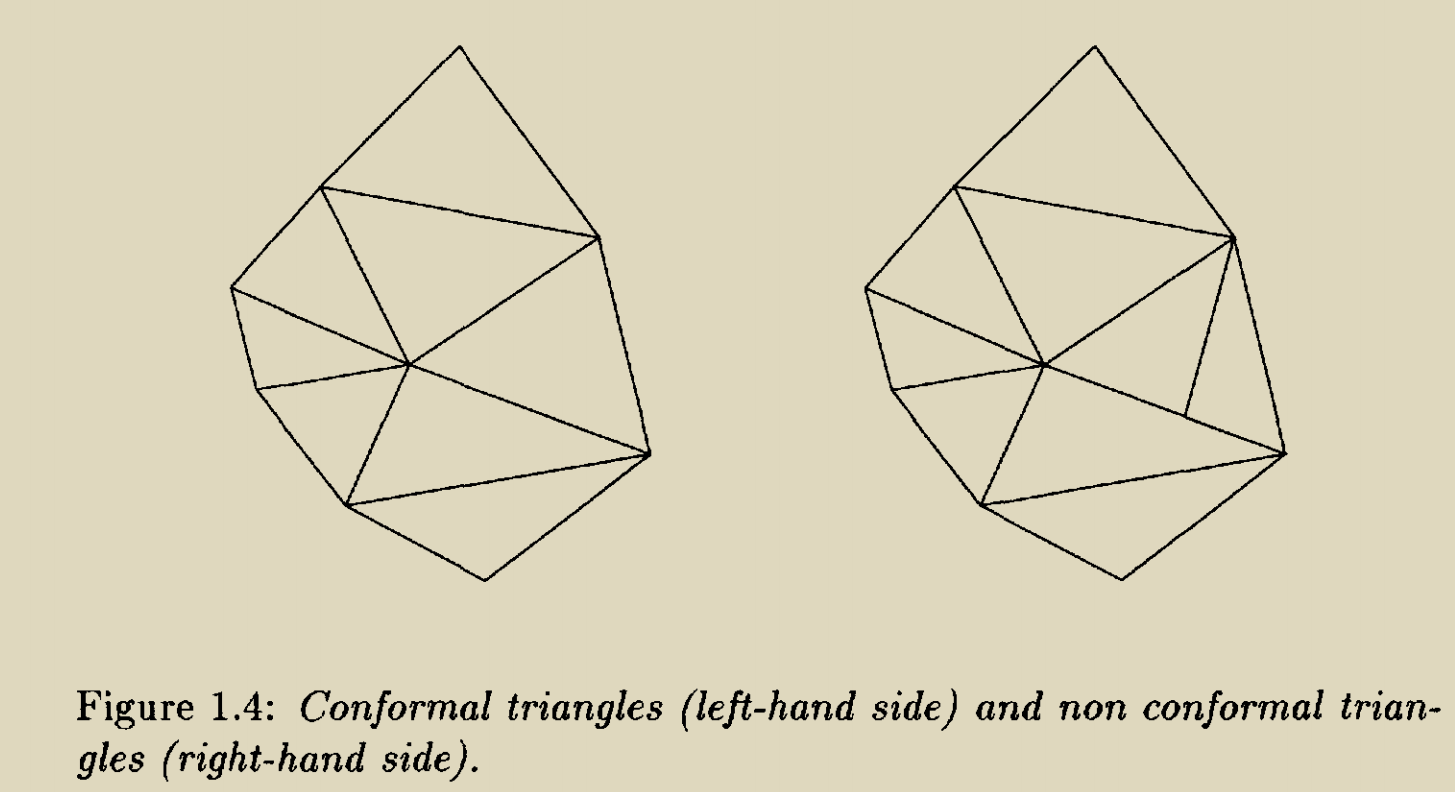
共形和非共形的三角形，如上图。

cste = 1，对于一个球

cste = 0，对于一个环

cste = 2，对于一个球有一个特殊的孔洞

因此在二维中，如果这有一个孔洞在三角化中，如果连接的组件的边界只有一个。$ns - na + ne = 1$

连接关系$na_f - 2 \times na_i + 3 \times ne = 0$ (ne) 是元素的数量，($na_i$)是内部边的数量，($na_f$)是外部边界的数量。

在三维中，一个三角化是一个封闭的面满足关系$ns - na + nf = 2$ (ns) 边界点在三角化过程中，na是边界边，nf是边界面。

空圆特性

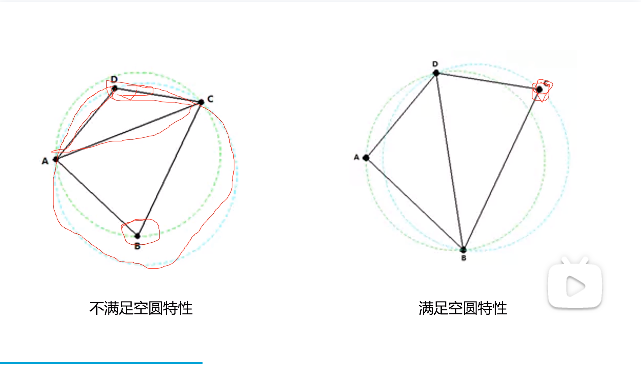
即一个三角形的外接圆不包含相邻三角形的顶点。满足空圆特性的三角形的最小角一定大于不满足空圆特性的最小角

Delaunay剖分具有的优异特性：

最接近：以最近的散点形成三角形，且各线段（三角形的边）皆不相交。
唯一性：不论从区域何处开始扣减，最终豆浆得到一致的结果。
最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么最小角不会增大
最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网...
区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。
具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

网格的质量

$Q_{\mathcal{M}}=\max _{K \in \mathcal{T}_{h}} Q_{K}$ 其中$Q_{\mathcal{M}}$ 是网格中最差的元素。

3D的网格质量可以从2D中推导出来

$Q_{3 D} \approx \frac{\sqrt{2}}{2} Q_{2 D}+1-\frac{\sqrt{2}}{2}$