ORCA避障源码笔记

参考资料

https://gamma.cs.unc.edu/ORCA/publications/ORCA.pdf

https://gamma.cs.unc.edu/RVO2/

数学知识

1.向量的点乘 dotProduct，计算方法：1.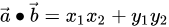   2.，

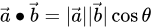作用：点积如果为负，则a,b形成的角为钝角；如果为零，那么a,b垂直；如果为正，那么a,b形成的角为锐角

2.向量a，向量b，det(a,b)表示行列式的值，计算方法x1y2 - x2y1，同时也是叉乘的值

作用：1.以两个向量为邻边的平行四边形的有向面积，2.小于0表示b在a的顺时针方向，大于0表示b在a逆时针方向，等于0表示a，b平行

下图是碰撞需要修正，并且保证最短修正的两种情况，

1) 将速度修正到切线上

2) 将速度修正到圆

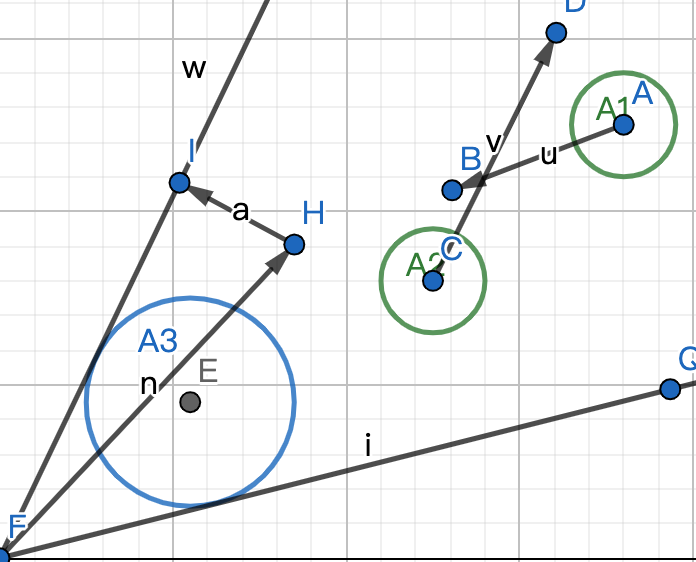
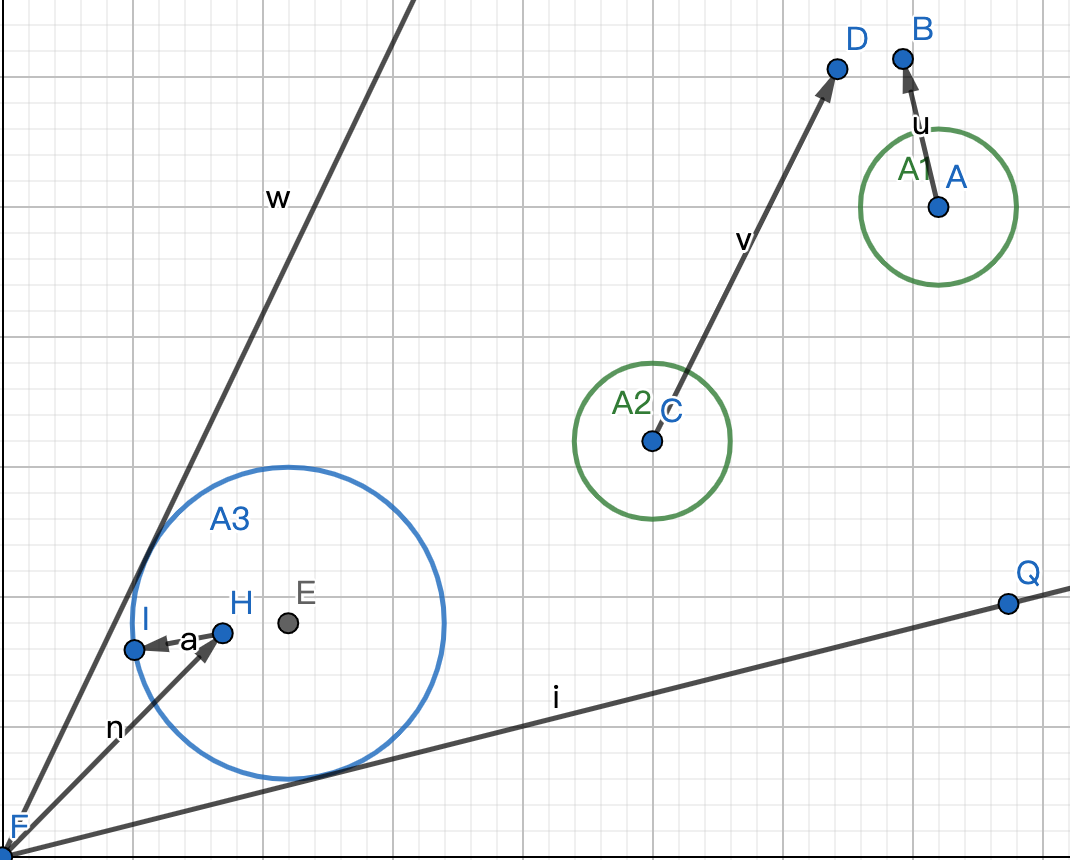
1，

final double dotProduct1 = w.dotProduct(relativePosition);

dotProduct1 < 0.0 && dotProduct1 * dotProduct1 > combinedRadiusSq * wLengthSq

这个代码是为了判断当前是哪种情况，

向量w = 相对速度 - 相对位置

dotProduct1小于0，表示向量w与相对位置的夹角为钝角，即AE与AO的角为锐角（需要先判断这个，只有锐角范围内cos单调递减）

dotProduct1 * dotProduct1 > combinedRadiusSq * wLengthSq，角OAE小于角OAD

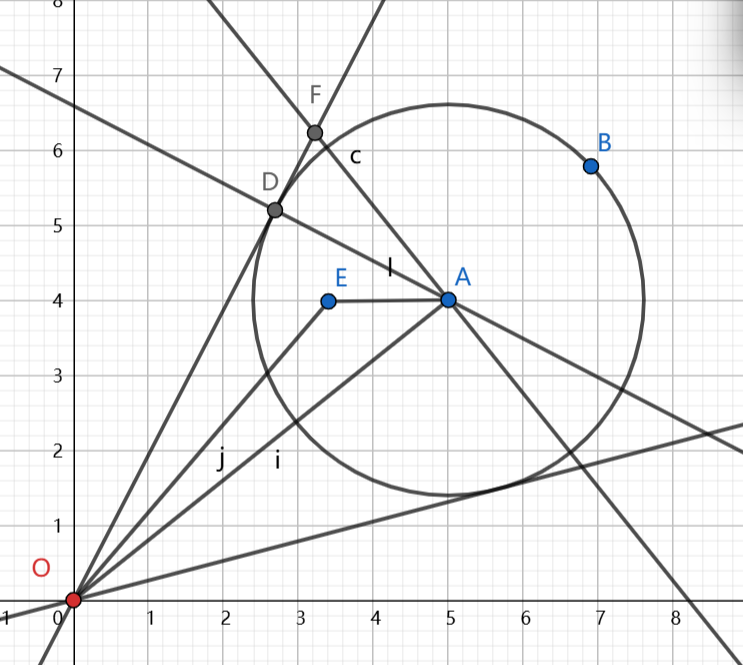
推导：

cos在0-90单调递减

角OAE < 角OAD

=> cosOAE > cosOAD

=> OA*cosOAE > OA*cosOAD  (同时乘以OA)

=> OA*cosOAE > AD (OA*cosOAD = AD)

=> OA * AE * cosOAE > AE * AD (同时乘以AE)

=> dotProduct1 * dotProduct1 > combinedRadiusSq * wLengthSq

2

direction = new Vector2D(relativePosition.getX() * leg - relativePosition.getY() * combinedRadius, relativePosition.getX() * combinedRadius + relativePosition.getY() * leg)

这段代码为了计算第一情况，修正速度的落点，

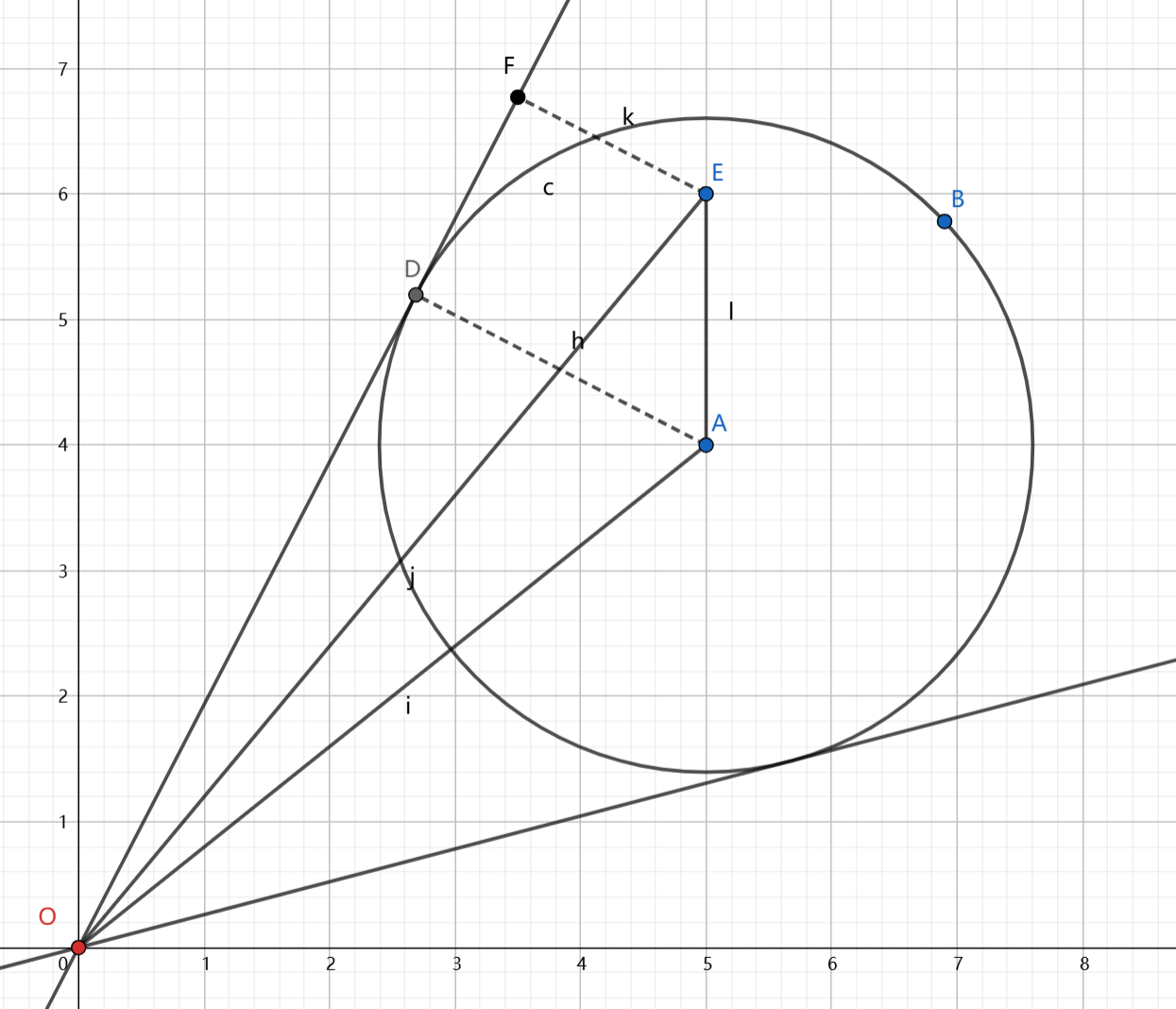
leg为OD的长度，假设direction为line的方向，即向量OD的单位向量DIR（a, b）顺时针的单位向量DIE (b, -a)，A的坐标(x, y)

向量OA 点乘 向量DIR = 向量OA的长度 * 1 * cosAOD

=> x*a + y*b = leg

向量OA 点乘 向量DIE = 向量OA的长度 * 1 * cosOAD

=>x*b - y*a = combinedRadius

结合这两个式子就可以解a，b，

RVOMath.det(relativePosition, w) > 0.0

这个在判断修正方向是在相对位置的左边还是右边

3

速度的可选区域为line方向的左侧， linearProgram2 找到可行域的交集，即line的交集

3.1

RVOMath.det(lines.get(lineNo).direction, lines.get(lineNo).point.subtract(newVelocity)) > 0.0

大于0说明newVelocity在line的右侧，不在line的可行域内，需要重新计算速度

3.2

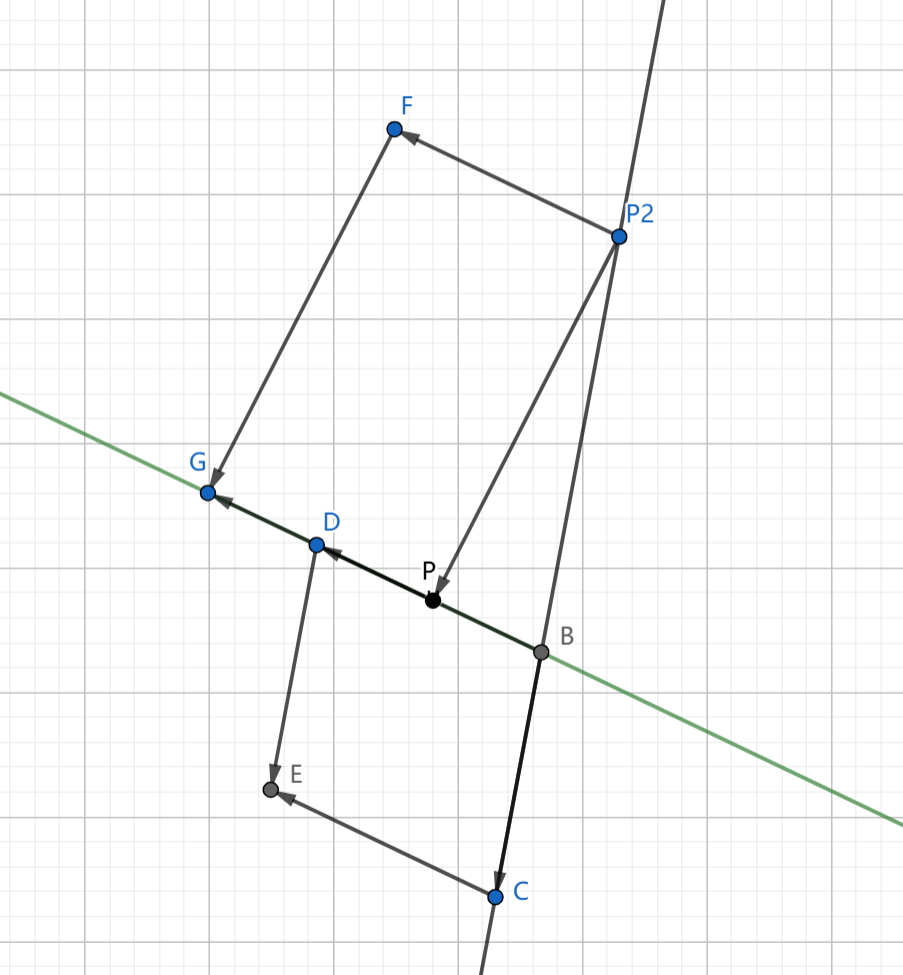
如图，绿色为line i, 黑色为line no

final double denominator = RVOMath.det(lines.get(lineNo).direction, lines.get(i).direction);
final double numerator = RVOMath.det(lines.get(i).direction, lines.get(lineNo).point.subtract(lines.get(i).point));
final double t = numerator / denominator;

denominator为BCED的面积 = 2个DBC的面积 = 2 * 1/2 * BP2 * 高

numerator为PGFP2的面积 = 2个GPP2 的面积 = 2个DBP2的面积 = 2 * 1/2 * BC * 高

t = numerator / denominator = BP2 / BC = BP2

t 为line i 和 line no 的交点 到 line point 的距离

4

linearProgram3

如果找不到line的交集，则执行linearProgram3，从上次失败的line开始往后遍历

将line i 之前的line做一个修正，修正的方法是：(1)将point修正到交点，(2)将方向修正到角平分线，靠近i的方向

RVOMath.det(lines.get(i).direction, lines.get(i).point.subtract(newVelocity)) > distance

这段代码用来判断是否需要修正速度，如果修正后的速度与当前line的距离大于前一个line的距离大，那么需要修正。

因为修正后速度将在角平分线上，一定距离当前line更近