MIT 18.06 Linear Algebra by Gilbert Strang

MIT 18.06 Linear Algebra by Gilbent Strang

Text and Solution: 《Introduction to Linear Algebra》

800x680

1The Geometry of Linear Equations

The fundamental problem of Linear Algebra which is to solve a system of linear equations.

讲解以一个方程组开始。

\[\left\{\begin{matrix}
2x - y = 0 \\
-x + 2y=3
\end{matrix}\right.
\]

如果我们学过线性代数，知道矩阵的乘法法则，就可以很自然的得出下面的等式。似乎也可以了解到矩阵乘法规则的由来。

\[A_{2\times 2} \times x_{2 \times 1}=
\begin{bmatrix}
2 &-1&\\
-1& 2&
\end{bmatrix}
\times
\begin{bmatrix}
x\\
y
\end{bmatrix}
=
\begin{bmatrix}
2x-y\\
-x+2y
\end{bmatrix}
=
\begin{bmatrix}
0\\
3
\end{bmatrix}\]

Understand by Row Picture：

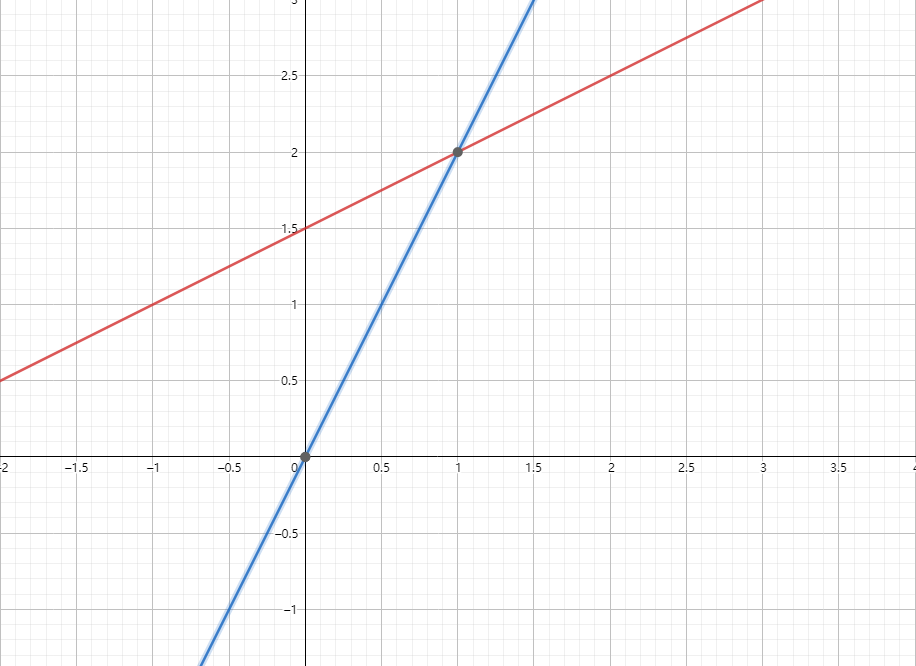
Understand by Column Picture：

\[A_{2\times 2} \times x_{2 \times 1}=
\begin{bmatrix}
2 &-1&\\
-1& 2&
\end{bmatrix}
\times
\begin{bmatrix}
x\\
y
\end{bmatrix}
=
x \begin{bmatrix}
2\\
-1
\end{bmatrix}
+
y \begin{bmatrix}
-1\\
2
\end{bmatrix}
=
\begin{bmatrix}
0\\
3
\end{bmatrix}\]

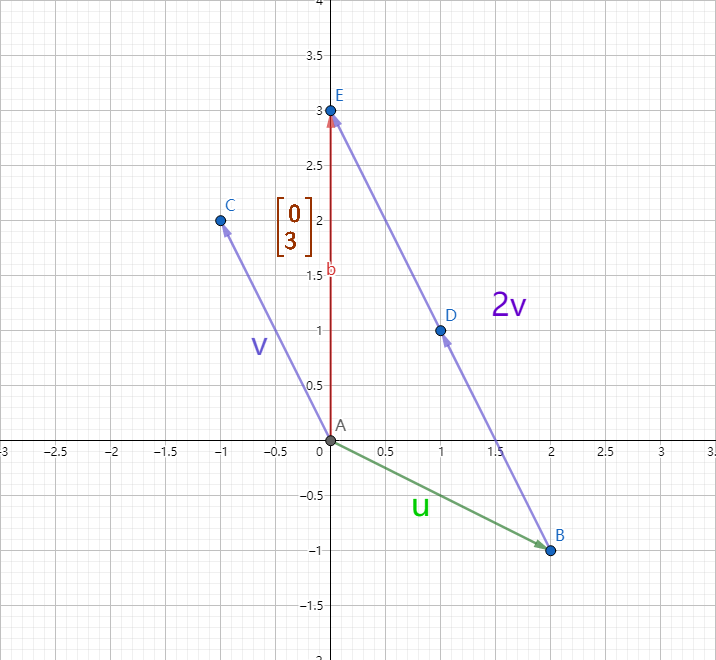
我们发现，方程组可以转换成向量空间中的一些向量的线性组合, 这些向量就是矩阵中的列向量。而这也是最重要的一点。

矩阵乘法的这种形式的表述真的是一种巨大的震撼。

两种解法都可以得到：

\[\begin{bmatrix}
x\\
y
\end{bmatrix} = \begin{bmatrix}
1\\
2
\end{bmatrix}
\]

Question

同时老师给出问题。假设现在是一个 3-D 空间。

Can I Solve \(Ax=b\) for every \(b\)?

or

Do the linear combination of the columns fill the 3-D space?

这个问题映射到上面的图中，以A中的3维列向量为基向量，它们的任意组合可不可以得到任意的3维向量 \(b\)？

在2维空间中，如果参加线性组合的向量处于同一条线上，不论怎么样都组合不出所有的2维向量。我们可以试着画一画。

同样在3维空间中，如果参加线性组合的列向量都处在一个平面之内，例如就在\((x,y,0)\)中，我们无论如何都组合不出所有的3-D向量，而只是在一个平面中不断的生长。

如果在同样在3维空间中，这3个列向量若是有两个是相等的，是重合在一起的，那么我们还能得到所有的3维向量\(b\)么？

结果是： A is a non-singular matrix, a invertible matrix. A 是非奇异的，可逆的矩阵！

\(Ax\) is a combination of columns of \(A\)!

这是老师希望的我们对于矩阵乘法的理解。

2 Elimination with Matrices

\[A_{3\times 3}=
\begin{bmatrix}
a_{11}& a_{12}& a_{13}\\
a_{21}& a_{22}& a_{23}\\
a_{31}& a_{32}& a_{33}
\end{bmatrix}
\;\;
a_{1\times 3}=
\begin{bmatrix}
x & y & z
\end{bmatrix}
\;\;
b_{3\times 1}=
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
\]

2.1 以行变换看待矩阵乘法

\[a_{1\times 3} \times A_{3\times 3}=
\begin{bmatrix}
x & y & z
\end{bmatrix}
\times
\begin{bmatrix}
a_{11}& a_{12}& a_{13}\\
a_{21}& a_{22}& a_{23}\\
a_{31}& a_{32}& a_{33}
\end{bmatrix}=
\begin{bmatrix}
xa_{11}+ya_{21}+za_{31}& xa_{12}+ya_{22}+za_{32}& xa_{13}+ya_{23}+ za_{33}\\
\end{bmatrix}\\
= x\begin{bmatrix} a_{11}& a_{12} & a_{13}\end{bmatrix} + y\begin{bmatrix}a_{21}& a_{22}& a_{23}& a_{12}\end{bmatrix} + z\begin{bmatrix} a_{31}& a_{32}& a_{33}\end{bmatrix}\\
=
\begin{bmatrix}
o & o&o\\
\end{bmatrix}\\
\]

\(xA\) is a combination of rows of \(A\)!

2.2 以列变换看待矩阵乘法

\[A_{3\times 3} \times b_{3 \times 1}=
\begin{bmatrix}
a_{11}& a_{12}& a_{13}\\
a_{21}& a_{22}& a_{23}\\
a_{31}& a_{32}& a_{33}
\end{bmatrix}
\times
\begin{bmatrix}
x\\
y \\
z
\end{bmatrix}
=
x \begin{bmatrix}
a_{11}\\
a_{21}\\
a_{31}
\end{bmatrix}
+
y \begin{bmatrix}
a_{12}\\
a_{22}\\
a_{32}
\end{bmatrix}
+
z \begin{bmatrix}
a_{13}\\
a_{23}\\
a_{33}
\end{bmatrix}
\]

\(Ax\) is a combination of columns of \(A\)!

2.3 矩阵乘法与方程组消元的关系

看待矩阵就要自然的与方程组联系在一起。

对于矩阵的一些变化，自然也要联系到方程组上来。之前说到，方程组的系数提取出来可以形成矩阵。

我们对于方程组的解法，通常是消元法。

例如3元1次方程组的解法就是不断的消去未知数。3元1次方程组，首先要消去1个未知数，接着得到2元1次方程组，2元1次方程组再消去1个未知数就得到了1元1次方程组。这就涉及到了系数的变化。

\[\left\{\begin{matrix}
x + 2y + z = 2 \\
3x + 8y +z=12\\
4y+z=2
\end{matrix}\right.
\]

1. row1*(-3) + row2
2. row2*(-2) + row3

\[\left\{\begin{matrix}
x + 2y + z = 2 \\
3x + 8y +z=12\\
4y+z=2
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x + 2y + z = 2 \\
2y -2z=6\\
4y+z=2
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x + 2y + z = 2 \\
2y -2z=6\\
5z=-10
\end{matrix}\right.
\]

\[\begin{bmatrix}
1 & 2 & 1\\
3 & 8 & 1\\
0 & 4 & 1
\end{bmatrix}
\begin{bmatrix}
2\\
12\\
2
\end{bmatrix}
\Rightarrow

\begin{bmatrix}
1 & 2 & 1\\
0 & 2 & -2\\
0 & 4 & 1
\end{bmatrix}
\begin{bmatrix}
2\\
6\\
2
\end{bmatrix}
\Rightarrow

\begin{bmatrix}
1 & 2 & 1\\
0 & 2 & -2\\
0 & 0 & 5
\end{bmatrix}
\begin{bmatrix}
2\\
6\\
-10
\end{bmatrix}
\]

通过对于矩阵乘法的行观点来看：

\[\begin{bmatrix}
1 & 0 & 0\\
-3 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 1\\
3 & 8 & 1\\
0 & 4 & 1
\end{bmatrix}
=
\begin{bmatrix}
1 & 2 & 1\\
0 & 2 & -2\\
0 & 4 & 1
\end{bmatrix}
\]

\[\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & -2 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0\\
-3 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 1\\
3 & 8 & 1\\
0 & 4 & 1
\end{bmatrix}
=
\begin{bmatrix}
1 & 2 & 1\\
0 & 2 & -2\\
0 & 0 & 5
\end{bmatrix}
\]

注意

A 左边的第一个矩阵对应着第一次的方程组的变换操作。

1. row1*(-3) + row2

A 左边的第二个矩阵对应着第二次的方程组的变换操作。

1. row2*(-2) + row3

而这种变换操作是可逆的不是么？ row1*(-3) + row2 的逆操作 是 row2 + row1*(3)。 因为矩阵对应变换操作，所以这个逆操作也可以转换成矩阵的形式！而这也就引出了逆矩阵！

\[\begin{bmatrix}
1 & 0 & 0\\
3 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0\\
-3 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}
\]

2.4 总结

左乘是行变换，右乘是列变换。

\[\begin{bmatrix}
0 & 1\\
1 & 0\\
\end{bmatrix}
\begin{bmatrix}
a& b\\
c & d\\
\end{bmatrix}
=
\begin{bmatrix}
c & d\\
a& b\\
\end{bmatrix}
\]

\[\begin{bmatrix}
a& b\\
c & d\\
\end{bmatrix}
\begin{bmatrix}
0 & 1\\
1 & 0\\
\end{bmatrix}
=
\begin{bmatrix}
b & a\\
d& c\\
\end{bmatrix}
\]