CF1737D Ela and the Wiring Wizard

CF1737D Ela and the Wiring Wizard

题意简述

形象化的，对于一个边，我们可以做以下变换：

1. 将一条边变为自环

   

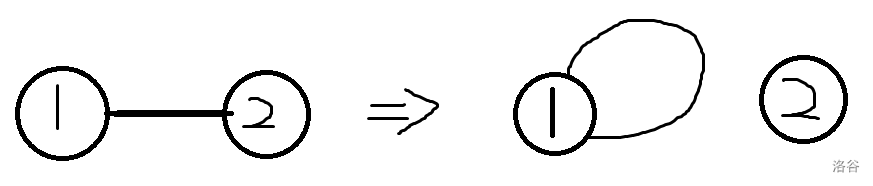
2. 将边的一个端点沿着其他边移动

   

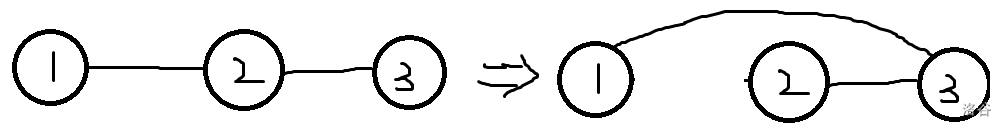
总的来说，就是边的两个端点可以自由移动

解释一下样例三：

$ (2,5),w=22\to(2,6),w=22\to(6,6),w=22\to(6,4),w=22\to(6,8),w=22\to(8,7),w=22\to(1,8),w=22 $

经过了 \(6\) 次变化，使得 \((1,8)\) 之间有连边，长度为 \(22\) ，最后走这条边，时间为 \(22\times7=154\)

思路

提出一个猜想：最小花费方案中，必然有一种是将一条边移动到 \(1,n\) 之间，然后走这条边。

证明的话（不会），感性理解就好了（我也是看样例猜出来的）

于是问题转化：考虑每一条边，求将其移动到 \(1,n\) 两边的最小走多少步 \(cnt\) 。我们求得便是 \(\min(w_i*(cnt+1))\)

对于一条边 \((x,y)\)

1. 其端点自己直接走到 \(1/n\)

   \(cnt=\min(dis_{x,1}+dis_{y,n},dis_{y,1}+dis_{x,n})\)

2. 其中一个端点先走到某一个中间点 \(s\) ，然后将另一个端点通过变换一接过来，再走去 \(1/n\)

   \(cnt=\min(dis_{x,s},dis_{y,s})+dis_{1,s}+dis_{s,n}+1\)

对于 \(dis\) 直接弗洛伊德就可以了

CODE

// #pragma GCC optimize("Ofast")
// #pragma GCC optimize("inline")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef long double ld;
const ll maxn=500+2;

inline ll read_int(){
	ll a=0;bool f=0;char g=getchar();
	while(g<'0'||g>'9') {if(g=='-') f=1;g=getchar();}
	while('0'<=g&&g<='9') a=a*10+g-'0',g=getchar();
	return f ? -a : a;
}

inline void write(ll a,bool f=1){
	char lin[40];ll top=0;
	if(a<0) a=-a,putchar('-');
	while(a) lin[++top]=a%10+'0',a/=10;
	if(!top) lin[++top]='0';
	while(top) putchar(lin[top--]);
	if(f) putchar('\n');
}

int n,m;

int mapp[maxn][maxn];
struct E{int f,t;ll v;}edge[maxn*maxn];

inline void read(){
    n=read_int(),m=read_int();
    memset(mapp,0x3f,sizeof mapp);
    for(int i=1;i<=n;i++) mapp[i][i]=0;
    for(int i=1;i<=m;i++){
        edge[i].f=read_int(),edge[i].t=read_int(),edge[i].v=read_int();
        mapp[edge[i].t][edge[i].f]=mapp[edge[i].f][edge[i].t]=1;
    }
    for(int i=1;i<=n;i++){
        for(int e=1;e<=n;e++){
            for(int j=1;j<=n;j++){
                mapp[e][j]=min(mapp[e][i]+mapp[i][j],mapp[e][j]);
            }
        }
    }
    ll ans=1e18;
    for(int i=1;i<=m;i++){
        int lin=min(mapp[edge[i].f][1]+mapp[edge[i].t][n],mapp[edge[i].f][n]+mapp[edge[i].t][1]);
        for(int e=1;e<=n;e++){
            lin=min(lin,min(
                mapp[edge[i].f][e],mapp[edge[i].t][e]
            )+mapp[e][1]+mapp[e][n]+1);
        }
        lin++;
        ans=min(ans,lin*edge[i].v);
    }
    write(ans);
}

int main (){
    // freopen(".in","r",stdin);
    int T=read_int();
    while(T--) read();
}