AGC018

AGC018

B

题目大意

举办一场运动会，有 \(N\) 人，\(M\) 个项目，每个人所有项目都有一个排名，会选择参加排名最高且开设的项目，现在要开设若干项目使得人数最多的项目人数尽可能小，求这个最小值。

解题思路

考虑贪心。

一开始，我们不妨开设所有项目，设人数最多的项目为 \(x\)。

如果我们不关闭项目 \(x\)，最大值就不会变，因此我们考虑关闭项目 \(x\)，将原来参加 \(x\) 的人分配到他们排名次高的项目（可以用 vector 存储参加这个项目的人）。

于是，又会有新的人数最多的项目，我们重复这个过程，直到只剩下一个项目，期间最大值的最小值即为答案。

注意：在重新分配项目时，不仅要根据次高排名，还要判断这个项目现在是否开设，不开设还要再往后。

时间复杂度：\(O(nm)\)

代码

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;

const int N = 310;

int n, m, ans;
int a[N][N], b[N][N], sz[N];
vector<int> e[N];
bool vis[N];

inline void add(int u, int v)
{
	e[u].push_back(v);
	sz[u]++;
}

int main()
{
	ios :: sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> a[i][j];
			b[i][a[i][j]] = j;
			if (j == 1)
			{
				add(a[i][j], i);
			}
		}
	}
	for (int i = 1; i <= m; i++)
	{
		if (!vis[i])
		{
			ans = max(sz[i], ans);
		}
	}
	for (int i = 1; i < m; i++)
	{
		int x = 0, mx = 0;
		for (int i = 1; i <= m; i++)
		{
			if (!vis[i])
			{
				if (sz[i] > mx)
				{
					mx = sz[i];
					x = i;
				}
			}
		}
		ans = min(mx, ans);
		for (auto it : e[x])
		{
			int v = b[it][x] + 1;
			while (vis[a[it][v]])
			{
				v++;
			}
			add(a[it][v], it);
		}
		vis[x] = 1;
	}
	cout << ans << endl;
	return 0;
}

C

题目大意

有 \(x+y+z\) 个人，第 \(i\) 个人有 \(A_i\) 个金币，\(B_i\) 个银币，\(C_i\) 个铜币。

要选出 \(x\) 个人获得其金币，选出 \(y\) 个人获得其银币，选出 \(z\) 个人获得其铜币。在不重复选某个人的情况下，求最大的获得的币的总数。

解题思路

考虑反悔贪心。

一开始有三个元素：金币、银币、铜币，较难处理。

考虑反悔机制，直接默认所有人都拿金币，之后把 \(y\) 人改成银币，选出 \(z\) 个改成铜币即可。

具体地，把金币个数加到答案里，再把每个人的信息改成二元组 \((B_i-A_i,C_i-A_i)\)，使得在选金币后再选这两个元素之一和选银币或铜币等价。

记 \(D_i=B_i-A_i\)，\(E_i=C_i-A_i\)，问题转化为在 \(N\) 个二元组中选 \(y\) 个 \(D_i\) 收益，选 \(z\) 个 \(E_i\) 收益，求最大的总收益。

考虑何时 \((D_i,E_i)\) 选 \(D_i\)、\((D_j,E_j)\) 选 \(E_j\) 不比 \((D_i,E_i)\) 选 \(E_i\)、\((D_j,E_j)\) 选 \(D_j\) 劣。

即 \(D_i+E_j\ge D_j+E_i\)，移项得：\(D_i-E_i\ge D_j-E_j\)。

于是我们可以按 \((D_i,E_i)\) 从大到小排序，此时前面一段统一选 \(D_i\)，后面一段统一选 \(E_i\) 一定不劣。

然后可以用优先队列维护前缀最大的 \(y\) 个 \(D_i\) 的和 \(s[i]\)，后最大的 \(y\) 个 \(D_i\) 的和 \(t[i]\)。

答案即为：

\[\sum A+\max_{i=y}^{n-z}(s[i]+t[i+1])
\]

时间复杂度 \(O(\log n)\)

代码

#include<bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;

const int N = 1e5 + 10;

struct node
{
	int a, b;
} p[N];

int n, x, y, z;
ll ans, s[N], t[N];
priority_queue<ll, vector<ll>, greater<ll> > q;

bool cmp(node x, node y)
{
	return x.a - x.b > y.a - y.b;
}

int main()
{
	ios :: sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> x >> y >> z;
	n = x + y + z;
	for (int i = 1; i <= n; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		ans += a;
		p[i].a = b - a, p[i].b = c - a;
	}
	sort(p + 1, p + n + 1, cmp);
	for (int i = 1; i <= n; i++)
	{
		s[i] = s[i - 1] + p[i].a;
		q.push(p[i].a);
		if ((int)q.size() > y)
		{
			s[i] -= q.top();
			q.pop();
		}
	}
	while (!q.empty())
	{
		q.pop();
	}
	for (int i = n; i >= 1; i--)
	{
		t[i] = t[i + 1] + p[i].b;
		q.push(p[i].b);
		if ((int)q.size() > z)
		{
			t[i] -= q.top();
			q.pop();
		}
	}
	ll mx = LONG_LONG_MIN;
	for (int i = y; i <= n - z; i++)
	{
		mx = max(mx, s[i] + t[i + 1]);
	}
	cout << ans + mx << endl;
	return 0;
}

D

题目大意

给出一棵有 \(N\) 个点有边权的无根树，现有一个有 \(N\) 个点的完全图，两点间边权即为他们在树上的简单路径长度，求这个图最长的哈密顿路径的长度。

解题思路

先考虑最长哈密顿回路长度。

要使其最长，就需要尽可能多地经过每一条边，考虑树上一条边能做出的最大贡献。

设这条边为 \((u,fa)\)，由于是哈密顿回路，有出有进且不能重复访问点，可以得到访问次数上界为 \(2\min(size_u,n-size_u)\)。

考虑能否让每条边取到这个上界，假设子树的点数小于子树外点数，可以发现取到上界时不能有路径在子树内部，因为子树点数本来就少，又被自己匹配掉一些，就会使经过这条边的最大次数减少，如果大于同理，也不能有路径完全在子树外。

为了方便讨论，我们不妨钦定重心为树根（如果重心有两个就可以缩点成一个），根据重心的性质，不会有子树点数大于子树外点数的情况，就避免了考虑另一种情况。

于是可以得到：不能有路径在一个子树内部，即每条路径都要经过重心，就可以取到最值（补充：一个重心可以就只在达重心上，两个重心必须经过连接两个重心的边），我们只需将答案加上最值即可。

现在我们考虑哈密顿路径，就是在回路的基础上减去一条最短的路径。

• 一个重心：此时最小值一定是在终点在重心上，那么就可以钦定连接重心的最小边为最后一条边，删去它损失必定最小
• 两个重心：由于两个重心必须经过连接两个重心的边，那么最短的路径即恰好为连接两个重心的边。

时间复杂度：\(O(n)\)

关于讨论区问题的补充：

证明最大哈密顿回路去掉最小边一定是最大哈密顿路径。

如果它不是最大哈密顿回路，即存在在同一棵子树的路径，由于一条路径会匹配掉两个点，那么就会使得经过的连接重心的边的访问次数减 \(2\)。

如图，中间的边少访问了两次：（非原创，侵删）

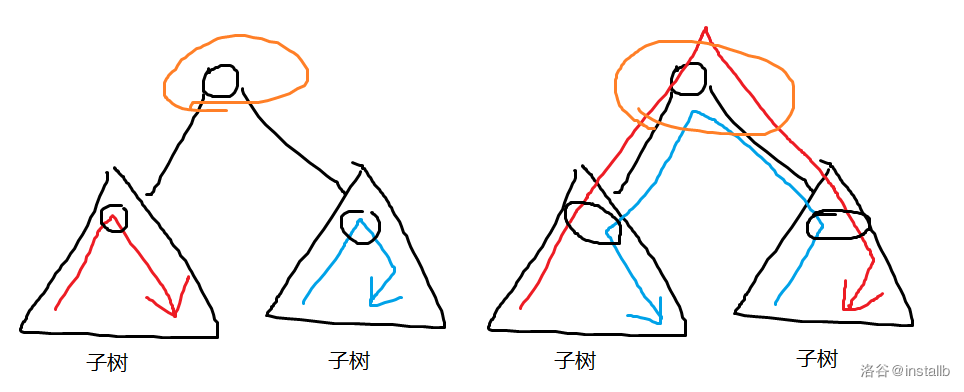
因为少了两次，而我们的哈密顿路径选取了最小的边，只少一次，因此它的哈密顿回路已经小于最大的哈密顿路径，所有哈密顿路径更小于最大的哈密顿路径。

代码

#include<bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;

const int N = 1e5 + 10;

struct edge
{
	int to, w, next;
} e[N << 1];

ll n, tot, ans, p1, p2;
ll h[N], sz[N], mx[N];

void add(int u, int v, int w)
{
	tot++;
	e[tot].to = v;
	e[tot].w = w;
	e[tot].next = h[u];
	h[u] = tot;
}

void dfs(int u, int fa)
{
	sz[u] = 1;
	for (int i = h[u]; i; i = e[i].next)
	{
		int v = e[i].to;
		if (v == fa)
		{
			continue;
		}
		dfs(v, u);
		sz[u] += sz[v];
		mx[u] = max(mx[u], sz[v]);
		ans += 2 * min(sz[v], n - sz[v]) * e[i].w;
	}
	mx[u] = max(mx[u], n - sz[u]);
}

int main()
{
	ios :: sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n;
	for (int i = 1; i < n; i++)
	{
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w), add(v, u, w);
	}
	dfs(1, 0);
	ll mn = LONG_LONG_MAX;
	for (int i = 1; i <= n; i++)
	{
		mn = min(mn, mx[i]);
	}
	for (int i = 1; i <= n; i++)
	{
		if (mx[i] == mn)
		{
			if (!p1)
			{
				p1 = i;
			}
			else
			{
				p2 = i;
			}
		}
	}
	mn = LONG_LONG_MAX;
	for (int i = h[p1]; i; i = e[i].next)
	{
		int v = e[i].to;
		if (p2 && v != p2)
		{
			continue;
		}
		mn = min(mn, (ll)e[i].w);
	}
	cout << ans - mn << endl;
	return 0;
}