BZOJ 4229: 选择 LCT_独创方法_边双

考虑如果两点在一个环中，那么这两点一定可以构出双联通分量.

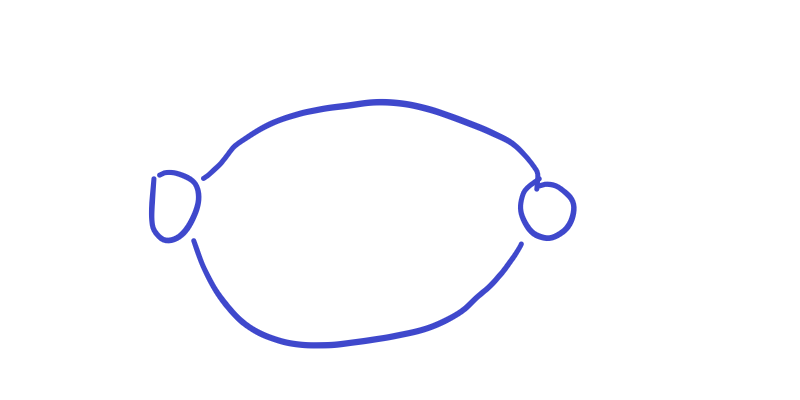
考虑环和环镶嵌，那么两个环中的点一定都互为双联通分量.

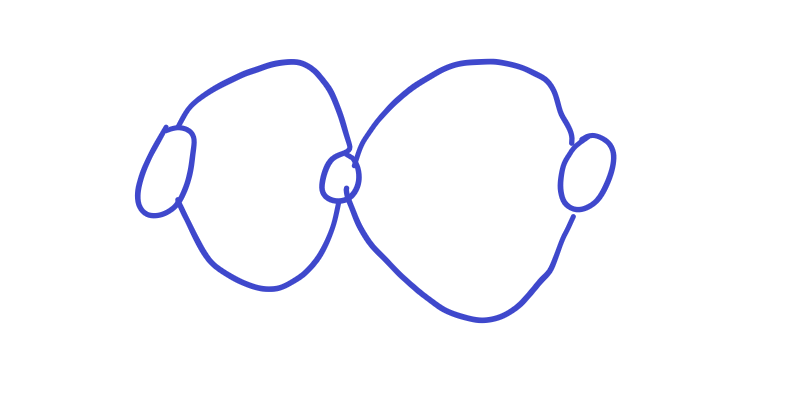
由此，我们想到一个算法：

将删边转为反向加边，用LCT维护图.

当我们连接两个点时，分两种两种情况.

1.不连通 : 没啥说的，直接连上

2.连通 : 那么说明要被连接的两点在一个换中，如下图：

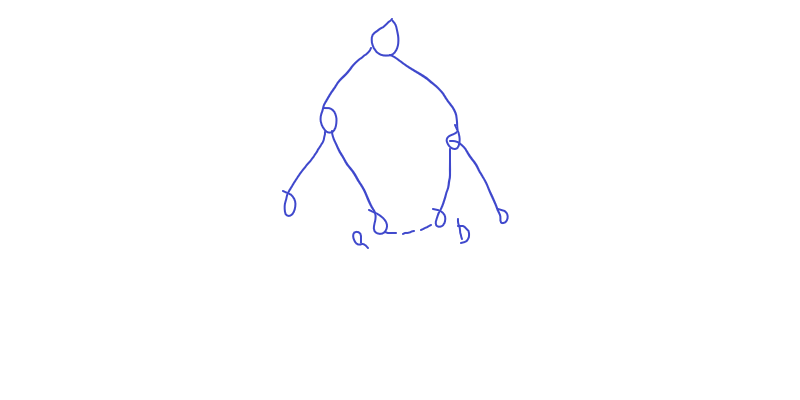
显然，整条路径上的所有点都互为双连通.

不过，与其维护点，我们维护边，将两点间所有边都设成 1.

在查询两个点是否为双联通时看看边权和是否等于边数即可(想一想，为什么 ? )

因为两点间的边都被赋值，有两种情况:

1. 两点为环，被统一赋值，显然正确.

2. 这条链被多个段落所覆盖，段落与段落之间至少有一个公共点，符合上述第二个结论，显然正确.

Code:

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <set>
#include <string>
#define setIO(s) freopen(s".in","r",stdin) ,freopen(s".out","w",stdout)
#define inf 1000000000
#define maxn 300007
#define pr pair<int,int>
using namespace std;
set <pr> b;
struct Union{
    int p[maxn];
    void init(){ for(int i=0;i<maxn;++i) p[i]=i;  }
    int find(int x){ return p[x]==x ? x : p[x]=find(p[x]);}
    int merge(int a,int b){
        int x=find(a),y=find(b);
        if(x==y) return 1;
        p[x]=y;
        return 0;
    }
}tree;
int tot;
int ans[maxn];
int ch[maxn][2],f[maxn],val[maxn];
int sta[maxn],tag[maxn],sumv1[maxn],addv[maxn],sumv2[maxn];
int lson(int x){ return ch[x][0]; }
int rson(int x){ return ch[x][1]; }
int get(int x){ return ch[f[x]][1]==x; }
int isRoot(int x){ return !(ch[f[x]][0]==x||ch[f[x]][1]==x); }
void mark(int x){ if(x) swap(ch[x][0],ch[x][1]),tag[x]^=1; }
void update(int x){ sumv1[x]=sumv2[x],addv[x]=1,val[x] = 1; }
void pushdown(int x){
    if(tag[x]) mark(lson(x)), mark(rson(x)), tag[x]=0;
    if(addv[x]) update(lson(x)),update(rson(x)),addv[x]=0;
}
void pushup(int x){
    sumv1[x]=sumv1[lson(x)]+sumv1[rson(x)] + val[x];
    sumv2[x]=sumv2[lson(x)]+sumv2[rson(x)] + 1;
}
void rotate(int x) {
    int old=f[x],oldf=f[old],which=get(x);
    if(!isRoot(old)) ch[oldf][ch[oldf][1]==old]=x;
    ch[old][which]=ch[x][which^1],f[ch[old][which]]=old;
    ch[x][which^1]=old,f[old]=x,f[x]=oldf;
    pushup(old),pushup(x);
}
void splay(int x){
    int v=0,u=x;
    sta[++v]=u;
    while(!isRoot(u)) sta[++v]=f[u],u=f[u];
    while(v) pushdown(sta[v--]);
    u=f[u];
    for(int fa;(fa=f[x])!=u;rotate(x))
        if(f[fa]!=u) rotate(get(fa)==get(x)?fa:x);
}

void Access(int x){ for(int y=0;x;y=x,x=f[x]) splay(x),ch[x][1]=y,pushup(x); }
void makeRoot(int x){ Access(x),splay(x),mark(x); }
void split(int x,int y){ makeRoot(x),Access(y),splay(y); }
void link(int a,int b){
    if(tree.merge(a,b) == 1) { makeRoot(a),Access(b),splay(b),update(b); }
    else{
        makeRoot(a);
        f[f[a]=++tot]=b;
    }
}
struct E{ int x,y; }err[maxn];
struct OPT{ int opt,x,y;  }opt[maxn];
char chf[10];
int main(){
    //setIO("input");
    int n,m,q;
    tot=100001;
    scanf("%d%d%d",&n,&m,&q),tree.init();
	for(int i=1;i<tot;++i) sumv1[i]=sumv2[i]=val[i]=1;
    for(int i=1;i<=m;++i) {
		scanf("%d%d",&err[i].x,&err[i].y);
		if(err[i].y>err[i].x) swap(err[i].x,err[i].y);
	}
    for(int i=1;i<=q;i++) {
        scanf("%s",chf);
        scanf("%d%d",&opt[i].x,&opt[i].y);
        if(opt[i].y>opt[i].x) swap(opt[i].x,opt[i].y);
        if(chf[0]=='Z')
        {
            opt[i].opt=1;
            b.insert(make_pair(opt[i].x,opt[i].y));
        }
        else opt[i].opt=0;
    }
    for(int i=1;i<=m;i++)
    {
        if(b.find(make_pair(err[i].x,err[i].y))==b.end())
        {
            link(err[i].x,err[i].y);
        }
    }
    for(int i=q;i>=1;--i) {
        if(opt[i].opt==1) { link(opt[i].x,opt[i].y);  }
        else {
            int a=opt[i].x,b=opt[i].y;
            if(tree.find(a)!=tree.find(b)) {ans[i]=0;continue; }
            makeRoot(a),Access(b),splay(b);
            if(sumv1[b]==sumv2[b]) ans[i]=1;
            else ans[i]=0;
        }
    }
    for(int i=1;i<=q;++i)
        if(opt[i].opt==0) {
            if(ans[i]==1) printf("Yes\n");
            else printf("No\n");
        }
    return 0;
}