Codeforces_765_D. Artsem and Saunders_(数学)

D. Artsem and Saunders

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Artsem has a friend Saunders from University of Chicago. Saunders presented him with the following problem.

Let [n] denote the set {1, ..., n}. We will also write f: [x] → [y] when a function f is defined in integer points 1, ..., x, and all its values are integers from 1 to y.

Now then, you are given a function f: [n] → [n]. Your task is to find a positive integer m, and two functions g: [n] → [m], h: [m] → [n], such that g(h(x)) = x for all 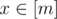, and h(g(x)) = f(x) for all , or determine that finding these is impossible.

Input

The first line contains an integer n (1 ≤ n ≤ 105).

The second line contains n space-separated integers — values f(1), ..., f(n) (1 ≤ f(i) ≤ n).

Output

If there is no answer, print one integer -1.

Otherwise, on the first line print the number m (1 ≤ m ≤ 106). On the second line print n numbers g(1), ..., g(n). On the third line print m numbers h(1), ..., h(m).

If there are several correct answers, you may output any of them. It is guaranteed that if a valid answer exists, then there is an answer satisfying the above restrictions.

Examples

input

3
1 2 3

output

3
1 2 3
1 2 3

input

3
2 2 2

output

1
1 1 1
2

input

2
2 1

output

-1[]
 
题意：f:[n]-->[m];g:[n]-->[m];h:[m]-->[n].给定n和f[1--n]的值，求一个m，使得g[h[x]]==x,h[g[x]]==f[x]。
 
比赛中看到这道题时，心里有点害怕，感觉做不出来，毕竟不太擅长这种题。然后第二天冷静了一下，AC掉。
 
思路：
由g[h[x]]==x和h[g[x]]==f[x]可知，只有当f[x]==x的x(或f[x])值可以做h[1--m]的值域中的元素，

所以由f[x]==x可以确定h[x]和m的值;有了h[x]，由h[g[x]]==f[x]可以确定g[x]。
 
并且h[1--m]的值域和f[1--n]的值域应该完全相同，否则不可能。因为若f[1--n]的值域中存在一个I，但不在h[1--m]的值域中，那么就存在一个

g[t]不能被确定。
 
不可能的情况什么时候发生？ 由以上思路，及由h[1--m]和f[1--n]若存在一个g[i]不能被确定，那么就是不可能的情况。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
#define N 100005
 
int f[N],g[N],h[N];
map<int,int>maph;
bool vis[N];
int main()
{
    int n,cntg;
    scanf("%d",&n);
    int m,last=;
    cntg=;
    for(int i=; i<=n; i++)
    {
        scanf("%d",&f[i]);
        if(f[i]==i)
        {
            vis[f[i]]=;
        }
    }
    //numg[cntg-1]+=n-last;
 
    m=;
    for(int i=; i<=n; i++)
        if(vis[i]==)
        {
            m++;
            h[m]=i;
            maph[i]=m;   //值域到定义域的映射
        }
    int flag=;
    for(int i=; i<=n; i++)
    {
        if(maph[f[i]]>)
            g[i]=maph[f[i]];
        else
            flag=;
    }
    if(flag)
    {
        printf("%d\n",m);
        for(int i=; i<=n; i++)
        {
            printf("%d",g[i]);
            if(i==n)
                printf("\n");
            else
                printf(" ");
        }
        for(int i=; i<=m; i++)
        {
            printf("%d",h[i]);
            if(i==m)
                printf("\n");
            else
                printf(" ");
        }
    }
    else
        printf("-1\n");
    return ;
}