haar的简单应用（1）

又双叒叕出现问题了，还是重置系统的原因，弄半天终于弄好了，就不说这个了

直接记录一下该做的

如下教程中的文件我倒是都找到了（但是这些文件在目前的代码中都用不到。。）

在这里

令我无语的他只用了一个.xml文件，而且还不在这里面，他的源代码如下

但是他用的这个default.xml文件并不在这里面，于是我找啊找

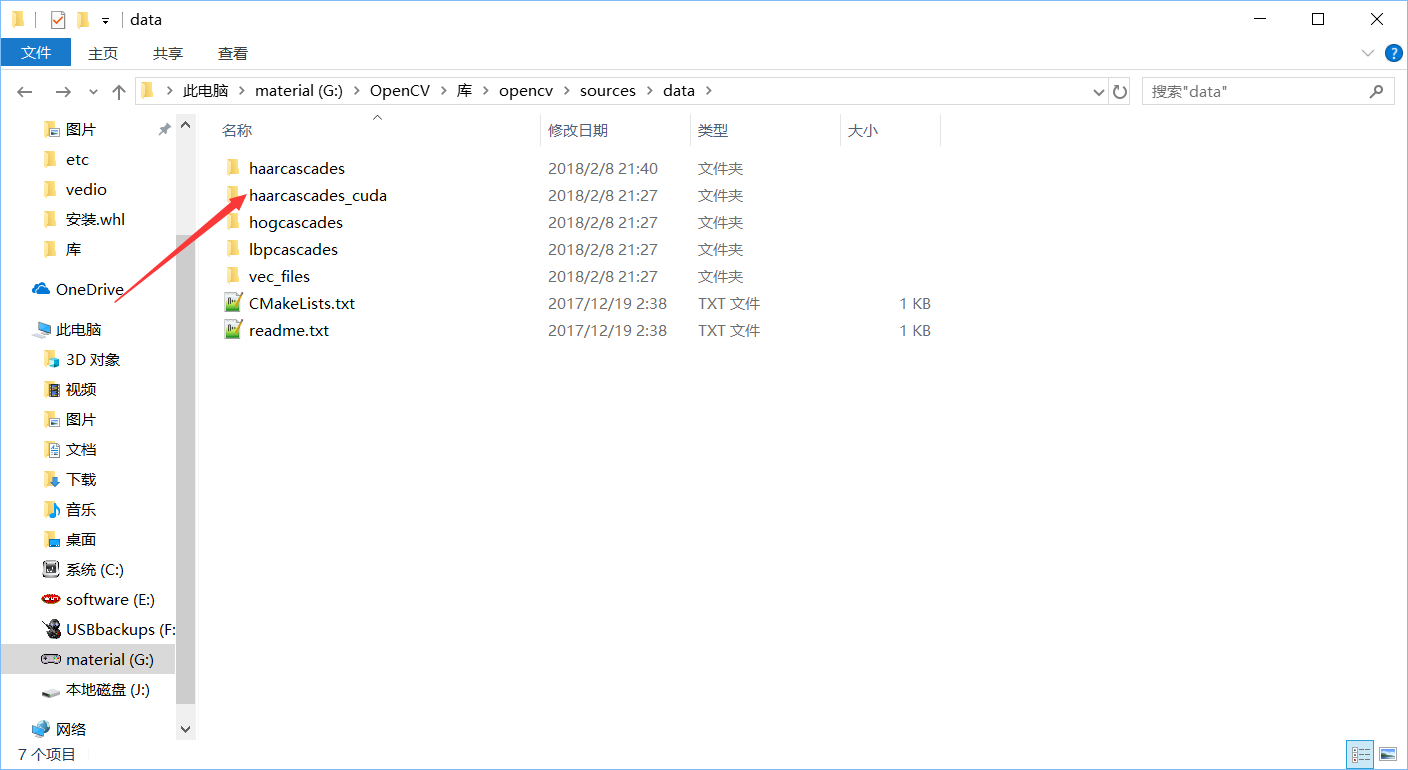
在他下面这个文件夹haarcascade_cuba里找到了haarcascade_frontalface_default.xml，在项目目录中新建一个文件夹cascade，拷贝过去

目录结构如下

全部代码

原理也很简单，直接使用它的分类器就行了（因为实现的是简单的人脸识别）

#已设置忽略  PEP8.E265

import cv2
filename = '../images/haar.jpg'

face_cascade = cv2.CascadeClassifier('../cascades/haarcascade_frontalface_default.xml')

img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

faces = face_cascade.detectMultiScale(gray, 1.3, 5)
for (x, y, h, w) in faces:
    img = cv2.rectangle(img,(x, y),(x + w, y + h), (255, 0, 0), 2)
cv2.namedWindow('faces Detected!')
cv2.imshow('faces Detected!', img)
cv2.imwrite('faces.jpg', img)
cv2.waitKey(0)

先试验了几个图片，运行结果如下

当年的热火三巨头，识别成功

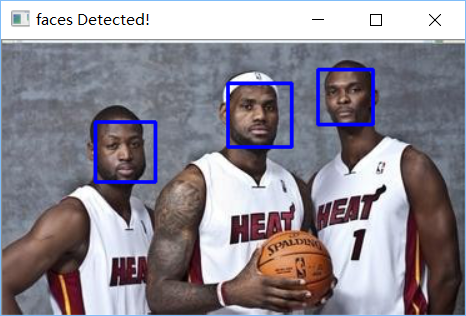
金州勇士的。。。难道肤色不统一的原因吗，毕竟就这么几行代码，能力还是有限

再具体的下回再说，今天就先弄了这点