POJ 1704 Georgia and Bob(阶梯Nim博弈)

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 11357		Accepted: 3749

Description

Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

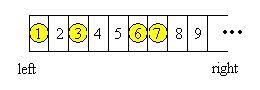Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win

Source

POJ Monthly--2004.07.18

[Submit]   [Go Back]   [Status]   [Discuss]

Home Page   Go Back  To top

这题做法真的666啊，不知道std是怎么想出来的

首先我们想到一种必败态：即仅有两个点且相邻

那么我们可以把所有的点排序之后两两捆绑，这样如果A移动第一个，那么B可以把第二个移动相同的步数

这样我们就解决了顺序的问题

那么接下来就考虑如何解决博弈问题

这里有个神仙操作

把两点直接的距离看做一堆石子，然后请Nim来就可以啦

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=1e4+,INF=1e9+;
inline int read()
{
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int a[MAXN];
int main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
    int QwQ=read();
    while(QwQ--)
    {
        int N=read();
        for(int i=;i<=N;i++) a[i]=read();
        sort(a+,a+N+);
        int ans;
        if(N&)//奇数
        {
            ans=a[]-;
            for(int i=;i<=N;i+=)
                ans=ans^(a[i]-a[i-]-);
        }
        else
        {
            ans=a[]-a[]-;
            for(int i=;i<=N;i+=)
                ans=ans^(a[i]-a[i-]-);
        }
        if(ans) printf("Georgia will win\n");
        else printf("Bob will win\n");
    }
    return ;
}