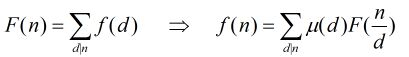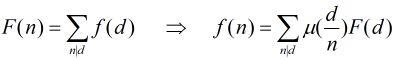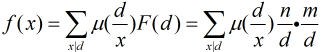HDU 1695 GCD (莫比乌斯反演模板)
GCD
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 17212 Accepted Submission(s): 6637
Problem Description
Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.
Yoiu can assume that a = c = 1 in all test cases.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.
Output
For each test case, print the number of choices. Use the format in the example.
Sample Input
2
1 3 1 5 1
1 11014 1 14409 9
Sample Output
Case 1: 9
Case 2: 736427
Hint
For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).
题解:
题意是求满足1<=x<=b和1<=y<=d的gcd(x,y)=k的(x,y)有多少对,可以转化为求1<=x<=b/k和1<=y<=d/k的gcd(x,y)=1的(x,y)有多少对,可以用到莫比乌斯反演解决,证明链接https://blog.csdn.net/outer_form/article/details/50588307
这里运用到第二个式子:
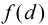
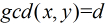
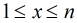
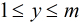
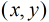
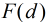
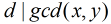
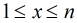
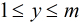
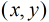
那么,一个数对x,y要满足它们的gcd是i的倍数,则x和y中都必须包含i这个因子,所以F(i)=⌊N/i⌋·⌊M/i⌋。所以反演后得到
所以得到 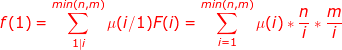
#include<iostream>
#include<string.h>
#define ll long long
using namespace std;
ll mu[100007],prime[100007];
bool mark[100007];
void getmu()
{
mu[1]=1;
ll cnt=0;
for(ll i=2;i<100007;i++){
if(!mark[i]){
prime[cnt++]=(ll)i;
mu[i]=-1;
}
for(ll j=0;j<cnt&&i*prime[j]<100007;j++){
mark[i*prime[j]]=1;
if(i%prime[j]){
mu[i*prime[j]]=-mu[i];
}else{
mu[i*prime[j]]=0;
break;
}
}
}
}
int main()
{
int T;
ll a,b,c,d,k,ans1,ans2;
getmu();
scanf("%d",&T);
for(int ca=1;ca<=T;ca++){
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
printf("Case %d: ",ca);
if(!k){printf("0\n");continue;}
b/=k,d/=k;
if(b>d) swap(b,d);
ans1=ans2=0;
for(ll i=1;i<=b;i++)
ans1+=mu[i]*(b/i)*(d/i);
for(ll i=1;i<=b;i++)
ans2+=mu[i]*(b/i)*(b/i);
printf("%lld\n",ans1-ans2/2);
}
return 0;
}
HDU 1695 GCD (莫比乌斯反演模板)的更多相关文章
- hdu 1695 GCD 莫比乌斯反演入门
GCD 题意:输入5个数a,b,c,d,k;(a = c = 1, 0 < b,d,k <= 100000);问有多少对a <= p <= b, c <= q <= ...
- HDU 1695 GCD 莫比乌斯反演
分析:简单的莫比乌斯反演 f[i]为k=i时的答案数 然后就很简单了 #include<iostream> #include<algorithm> #include<se ...
- hdu 1695 GCD 莫比乌斯
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- [BZOJ 2820] YY的gcd(莫比乌斯反演+数论分块)
[BZOJ 2820] YY的gcd(莫比乌斯反演+数论分块) 题面 给定N, M,求\(1\leq x\leq N, 1\leq y\leq M\)且gcd(x, y)为质数的(x, y)有多少对. ...
- HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- HDU 1695 GCD (莫比乌斯反演)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- hdu 1695: GCD 【莫比乌斯反演】
题目链接 这题求[1,n],[1,m]gcd为k的对数.而且没有顺序. 设F(n)为公约数为n的组数个数 f(n)为最大公约数为n的组数个数 然后在纸上手动验一下F(n)和f(n)的关系,直接套公式就 ...
- ●HDU 1695 GCD
题链: http://acm.hdu.edu.cn/showproblem.php?pid=1695 题解: 容斥. 莫比乌斯反演,入门题. 问题化简:求满足x∈(1~n)和y∈(1~m),且gcd( ...
- hdu1695(莫比乌斯反演模板)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1695 题意: 对于 a, b, c, d, k . 有 x 属于 [a, b], y 属于 [c, ...
随机推荐
- python正则表达式获取代理IP网站上的IP地址
import urllib.request import re def open_url(url): req = urllib.request.Request(url) req.add_header( ...
- Scala 继承
1. 继承 Scala 通过 extends 关键字来继承类. 那么继承一个类有什么好处呢? 子类拥有继承自超类的方法和字段(即为val(常量), var(变量)所定义的) 可以添加自己需要的新方法和 ...
- Keepalived详解(一):Keepalived介绍【转】
一.Keepalived介绍: Keepalived是Linux下一个轻量级的高可用解决方案,它与HeartBeat.RoseHA实现的功能类似,都可以实现服务或者网络的高可用,但是又 ...
- Windows PowerShell 入門(10)-デバッグ編
対象読者 Windows PowerShellでコマンドレット操作ができる方 何らかのプログラミング経験があればなお良い 必要環境 Windows PowerShell デバッグメッセージの出力 Po ...
- cocos开发学习记录
场景的创建和切换 https://blog.csdn.net/lin453701006/article/details/56334578
- [JLOI2011]飞行路线 不同的算法,不同的悲伤
题目 :BZOJ2763 洛谷P4568 [JLOI2011]飞行路线 一道最短路的题目,想想写个题解也不错(好久没写题解了_(:з」∠)_) 然后这道题中心思路是dijikstra处理最短路,所以没 ...
- less个人学习笔记
less中文官网:http://lesscss.cn/ . http://www.bootcss.com/p/lesscss/ Busy 视频教程:http://www.imooc.com/learn ...
- $Django redis内存数据库 (知识回顾cmd切换目录)
知识小回顾 #切换盘 C:\Users\WangDong>f: F:\> #切换文件 F:\>cd redis F:\redis> #返回上一级 F:\DJ\dj8>cd ...
- vuex之 mapState, mapGetters, mapActions, mapMutations 的使用
一.介绍 vuex里面的四大金刚:State, Mutations,Actions,Getters (上次记得关于vuex笔记 http://www.cnblogs.com/adouwt/p/8283 ...
- python学习第7天
编码的进阶 文件操作 深浅copy