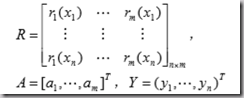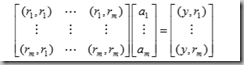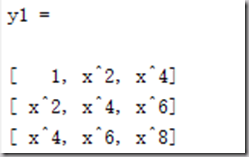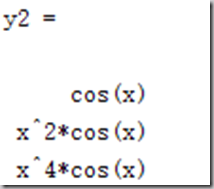【数学建模】day04-插值与拟合

关于插值原理，这篇文章里总结过。

插值，是在有限个数据点的情况下，模拟出更多的点来适应实际问题的需要。

拟合，是在已知数据点基础上，以已知点处最小误差为标准，模拟出近似函数。

二者有似，实则不同，matlab提供了基本完整的解决方案。

一、插值

1. 一维插值

(1)拉格朗日插值

经典的拉格朗日插值并没有现成的函数。自行编写如下：

input: 相同维度的已知点x0,y0

output：x点处的插值y

 function y = lagrange(x0,y0,x)
  % 函数：已知点组（x0,y0），求x出的插值y
  n = length(x0);
  m = length(x);
  for i = :m
      z=x(i);
      s=0.0;
      for k = :n
          p = 1.0;
          for j = :n
              if j~=k
                  p = p * (z-x0(j))/(x0(k)-x0(j));
              end
          end
          s = p*y0(k)+s;
      end
      y(i) = s;
  end

(2)MATLAB一维插值工具箱

通用: y = interp1(x0,y0,x,’method’)

param：

　　x0、y0：已知数据点。要求x0必须单调，x0等距时，使用快速插值。

　　x：要插值的点，内插。matlab外插产生不确定值。

　　method：规定插值方法

有：  'linear'：线性插值，如需要分段线性插值

'spline':  三次样条插值

'cubic' :  三次插值，如分段三次插值，即埃尔米特插值

'nearest':最近项插值，如果插值遇到外推产生不确定值，使用这个产生值去代替那些不确定值。

针对三次样条插值（常用），用法有：

• y = interp1(x0,y0,x,’spline’);
• y = spline(x0,y0,x);
• pp = csape(x0,y0,conds);
• pp = csape(x0,y0,conds,valconds), y = fnval(pp,x);%产生值

其中，D方法最常用，说明：

pp = csape(x0,y0,conds,valconds), y = fnval(pp,x)

param：

　　conds：指定插值的边界条件（三次样条插值需要2个边界条件）

'not-a-knot'：非扭结条件，即强迫第1、2和倒数1、2个多项式三次导数亦相等

'complete'：边界为一阶导数，一阶导数的值由valconds给出

'second'：边界为二阶导数，二阶导数值由valconds给出

'periodic' ：周期条件

　　valconds：见上，具体使用help csape

return：

　　返回pp对象，使用pp.coefs得到每个小区间上三次插值多项式的系数

　　 使用y = fnval(pp,x）得到x处的插值

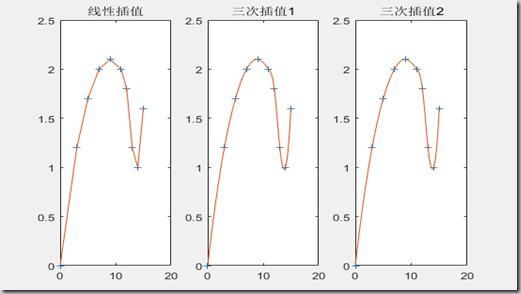
例子：分段线性以及三次插值，插值点如下

x	0	3	5	7	9	11	12	13	14	15
y	0	1.2	1.7	2.0	2.1	2.0	1.8	1.2	1.0	1.6

 x0 = [,,,,,,,,,];
  y0 = [,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
  x = :0.1:;
  y1 = interp1(x0,y0,x,'linear');%分段线性插值
 y2 = interp1(x0,y0,x,'spline');%三次插值
 pp1 = csape(x0,y0);
  y3 = fnval(pp1,x);
 pp2 = csape(x0,y0,'second');
  y4 = fnval(pp2,x);
  subplot(,,);
 % subplot(,,)是指
 %一个2行3列的图中从左到右从上到下的第一个位置
 plot(x0,y0,'+',x,y1);
  title('线性插值');
 subplot(,,);
  plot(x0,y0,'+',x,y2);
  title('三次插值1');
  subplot(,,);
  plot(x0,y0,'+',x,y3);
  title('三次插值2');

例：三次样条插值，并求出插值函数

　　样本点：

t	0.15	0.16	0.17	0.18
v	3.50	1.50	2.50	2.80

求解：

x0 = 0.15:0.01:0.18;
 y0 = [3.5,1.5,2.5,2.8];
 pp = csape(x0,y0);%默认条件是拉格朗日边界条件
format long g
 xishu = pp.coefs

xishu =

-616666.666666667                     33500         -473.333333333334                       3.5
         -616666.666666667                     15000          11.6666666666671                        1.5
         -616666.666666668         -3499.99999999999          126.666666666667              2.5

2. 二维插值

尤其是等高线绘制上，尤为重要。

二维插值特别注意维度问题。

matlab函数：

1、通用：z = interp2(x0,y0,z0,x,y,’method’)

param：

　　x0、y0：m维向量和n维向量，代表有m*n组数据点

　　z0：矩阵，n*m维，注意n是y0的维度

　　x、y:需要插值的点，注意x和y必须方向不同，表示有a*b组数据点

　‘method’：同一维

return：

　　z矩阵，行数是y的维数，列数是x的维数，表示对应点处的插值

2、三次样条插值：pp = csape({x0,y0},z0,conds,valconds)；

                        z = fnval(pp,{x,y})；

param：

　　{x0,y0}：x0是m维，y0是n维

　　z0：m*n矩阵，注意这里m是x0的维度

　　其他同一维

return:

　　fnval的参数{x,y}是m*n，返回z是插值，是m*n维矩阵。

 3、函数：插值节点为散乱点

　　ZI = griddata(x,y,z,XI,YI)

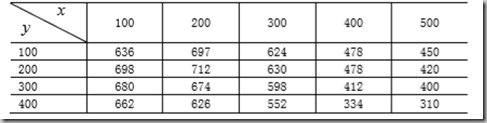
例：二次插值

已知高程部分点为：

每隔10m求插值点，并做曲面，求最高点

 clear,clc
  x = ::;
  y = ::;
  z=[               

                    ];
  pp = csape({x,y},z');
  xi = ::;
  yi = ::;
  cz = fnval(pp,{xi,yi});
  [i,j] = find(cz == max(max(cz)));%最大点的位置坐标,注意用法
 x = xi(i); %用位置坐标求对应的x值
 y = yi(j);
  zmax = cz(i,j);
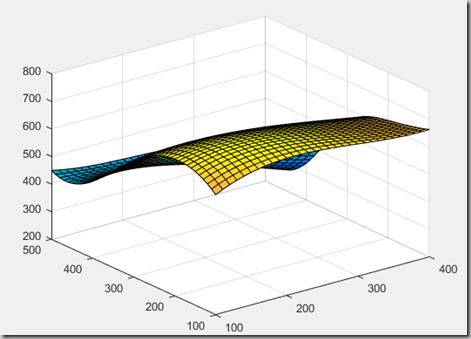
  [X,Y] = meshgrid(yi,xi);
  surf(X,Y,cz);hold on;

求得最高点是：(170,180)处，z = 720.6252；

二、曲线拟合

1. 曲线拟合的最小二乘法以及matlab求解

最常用。用f(x)拟合数据点(x,y)。使得平方误差[f(x)-y]^2之和最小。求偏导以求系数。问题规范为：

min ||RA-Y||₂²

R是线性无关函数组成的矩阵,A是系数，Y是x点处的y值向量。

那么，matlab的求解命令为：

A = R\Y.

理解：求这类问题就是，构造R矩阵，一般为r1(x)=1,r2(x)=x,r3(x)=x^2；代入拟合已知点x1,x2…xn求得这个矩阵，至于Y，就是拟合已知点处的y值。求得A就是需要的系数。

MATLAB对于m次多项式拟合的命令为：

a = polyfit(x0,y0,m)；y = polyval(a,x);%求x处的值

理解：利用（x0,y0）数值对，拟合m次多项式，规则为最小二乘规则。

matlab拟合工具箱：cftool命令打开。

注意：poly与plot区分。

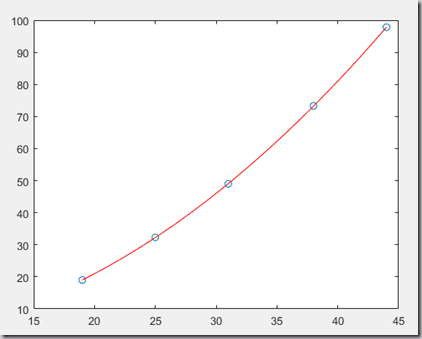
例子：拟合形如y = a + b*x^2的经验公式，数据如下：

 x = [,,,,]';
  y = [19.0,32.3,49.0,73.3,97.8]';
  %构造r矩阵
 r = [ones(,),x.^];
  ab = r\y;
  x0 = :0.1:;
  y0 = ab() + ab()*x0.^;
  plot(x,y,'o',x0,y0,'r');

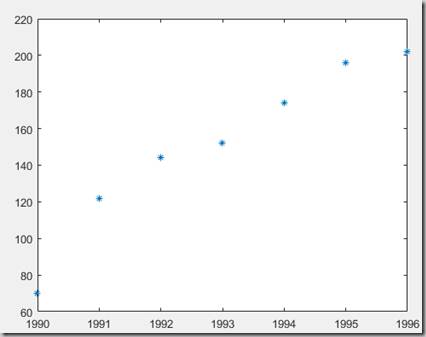
例子：利用matlab命令，拟合并画图。

分析:画散点图，分许趋势，选定多项式次数，求之。

x0 = ::;
 %x = x';
 y0 = [,,,,,,];
 plot(x0,y0,'*');
 %直线拟合
a = polyfit(x0,y0,);
 y97 = polyval(a,)
 y98 = polyval(a,)

y97 =

233.4286

y98 =

253.9286

2. 最小二乘优化

这类问题是无约束优化中，目标函数由若干个函数的平方构成。针对不同形式，有若干解决函数，比如：lsqlin、lsqcurvefit、lsqnonlin、lsqnonneg等。例子如下，用到查阅，不用记忆。

解决上面的例子：

拟合形如y = a + b*x^2的经验公式，数据如下：

3. 函数逼近的问题

这类问题是给定函数复杂， 但需对其分析，则可以用一个多项式（一般来说是这样）去逼近原函数。如何求这样的多项式函数。

问题规范为：

其中，y是被逼近函数的值，注意R矩阵的构造，(r1,r1)表示r1*r1。求系数向量a。

例：多项式函数H=span{1,x^2,x^4}逼近y =cos(x)，x∈[-pi/2,pi/2]；

syms x
 base = [,x.^,x.^];
 y1 = base.'*base
 y2 = cos(x)*base.'
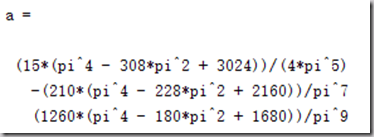
 r1 = int(y1,-pi/,pi/)
 r2 = int(y2,-pi/,pi/)
 a = r1\r2 %核心命令
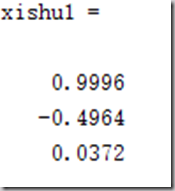
xishu1 = double(a)
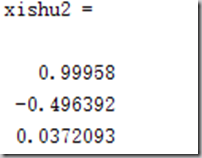
 xishu2 = vpa(a,)

其中注意：