反卷积（Transposed Convolution）

反卷积的具体计算步骤

令图像为

卷积核为

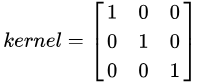
case 1

如果要使输出的尺寸是 5x5，步数 stride=2 ，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input,
                                        filter=kernel,
                                        output_shape=[1,5,5,1],
                                        strides=2,
                                        padding='SAME')

当执行 transpose_conv 命令时，tensorflow 会先计算卷积类型、输入尺寸、步数和输出尺寸之间的关系是否成立，如果不成立，会直接提示错误，如果成立，执行如下操作：

1. 现根据步数strides对输入的内部进行填充，这里strides可以理解成输入放大的倍数，即在input的每个元素之间填充 0，0的个数n与strides的关系为：n=strides-1

例如这里举例的strides=2，即在input的每个元素之间填1个0：

2. 接下来，用卷积核kernel对填充后的输入input_pad进行步长stride=1的正向卷积，根据正向卷积输出尺寸公式：  得到输出尺寸是5x5，反卷积公式中我们给出的输出尺寸参数output_shape也是为5，两者相同，所以可以进行计算，结果为：

与 tensorflow 的运行结果相同。

case 2

我们将 case 1 中的输出尺寸output_shape改成6，其他参数均不变，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input,
                                        filter=kernel,
                                        output_shape=[1,6,6,1],
                                        strides=2,
                                        padding='SAME')

卷积类型是 same，我们首先在外围填充一圈0：

这时发现，填充后的输入尺寸与3x3的卷积核卷积后的输出尺寸是5x5，没有达到output_shape的6x6，这就需要继续填充0，tensorflow 的计算规则是优先在左侧和上侧填充一排0，填充后的输入变为：

接下来，再对这个填充后的输入与3x3的卷积核卷积，结果为：

与 tensorflow 的运行结果相同。

参考资料：

https://zhuanlan.zhihu.com/p/48501100