洛谷 P3302 [SDOI2013]森林 解题报告

P3302 [SDOI2013]森林

题目描述

小\(Z\)有一片森林，含有\(N\)个节点，每个节点上都有一个非负整数作为权值。初始的时候，森林中有\(M\)条边。

小Z希望执行\(T\)个操作，操作有两类：

Q x y k查询点\(x\)到点\(y\)路径上所有的权值中，第\(k\)小的权值是多少。此操作保证点\(x\)和点\(y\)连通，同时这两个节点的路径上至少有\(k\)个点。

L x y在点\(x\)和点\(y\)之间连接一条边。保证完成此操作后，仍然是一片森林。

为了体现程序的在线性，我们把输入数据进行了加密。设\(lastans\)为程序上一次输出的结果，初始的时候\(lastans\)为\(0\)。

对于一个输入的操作Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。

对于一个输入的操作L x y，其真实操作为L x^lastans y^lastans。其中^运算符表示异或，等价于pascal中的xor运算符。

请写一个程序來帮助小Z完成这些操作。

对于所有的数据，\(n,m,T<=8*10^4\)

.

输入输出格式

输入格式：

第一行包含一个正整数\(testcase\)，表示当前测试数据的测试点编号。保证\(1<=testcase<=20\)。

第二行包含三个整数\(N\)，\(M\)，\(T\)，分别表示节点数、初始边数、操作数。

第三行包含\(N\)个非负整数表示 \(N\)个节点上的权值。

接下来 \(M\)行，每行包含两个整数\(x\)和\(y\)，表示初始的时候，点\(x\)和点\(y\)之间有一条无向边。

接下来 \(T\)行，每行描述一个操作，格式为”Q x y k“或者”L x y “，其含义见题目描述部分。

输出格式：

对于每一个第一类操作，输出一个非负整数表示答案。

说明：

---

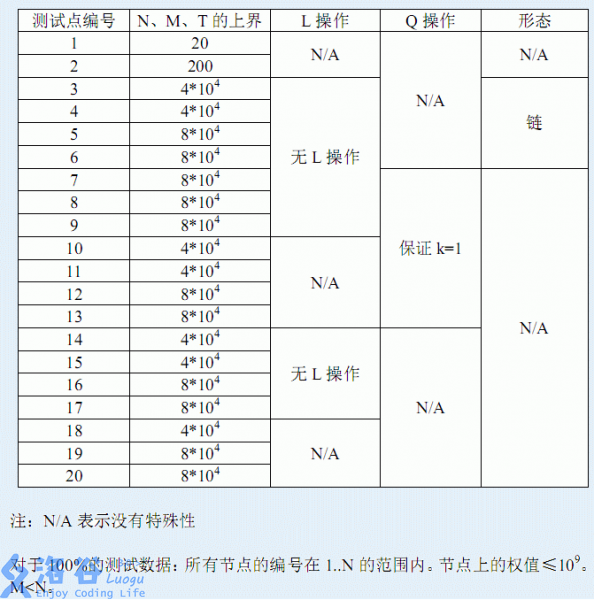
先吐槽：第一行原来给的是测试点编号我以为是数据组数还T了一会儿

动态维护树上两点间第\(k\)值

LCT不能直接维护第\(k\)值，也很难嵌套其他数据结构，所以我们不考虑她

发现只有加边没有删边，考虑使用主席树启发式合并

具体来说

加边时

把节点少的主席树合并到节点多的主席树上面，复杂度\(slogs\),\(s\)为小主席树的大小,同时动态更新父节点的倍增数组，复杂度也是\(slogs\)的

查询时

进入两个点以及它们的lca和lca的爹的主席树中上上下下加加减减

总复杂度：\(O(nlog^2n)\)

---

Code:

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ls ch[now][0]
#define rs ch[now][1]
#define ols ch[las][0]
#define ors ch[las][1]
const int N=3e5+10;
int ch[N*30][2],sum[N*30],tot;
int f[N][20],dep[N],n,m,n_,t,tmp,siz[N],root[N],a[N],b[N],testcase;
void updata(int now){sum[now]=sum[ls]+sum[rs];}
int rebuild(int las,int l,int r,int pos)
{
    int now=++tot;
    if(l==r) {sum[now]+=sum[las]+1;return now;}
    int mid=l+r>>1;
    if(pos<=mid)
    {
        ls=rebuild(ols,l,mid,pos);
        rs=ors;
    }
    else
    {
        ls=ols;
        rs=rebuild(ors,mid+1,r,pos);
    }
    updata(now);
    return now;
}
int head[N],to[N<<1],Next[N<<1],cnt;
void add(int u,int v)
{
    to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
}
int dfs(int now,int fa)
{
    int s=1;
    root[now]=rebuild(root[fa],1,n,b[now]);
    f[now][0]=fa;
    dep[now]=dep[fa]+1;
    for(int i=1;i<=18;i++)
        f[now][i]=f[f[now][i-1]][i-1];
    for(int i=head[now];i;i=Next[i])
        if(to[i]!=fa)
            s+=dfs(to[i],now);
    return s;
}
void swap(int &x,int &y){tmp=x,x=y,y=tmp;}
int rt(int now)
{
    for(int i=18;~i;i--)
        if(f[now][i])
            now=f[now][i];
    return now;
}
void Merge(int x,int y)
{
    int rx=rt(x),ry=rt(y);
    if(siz[rx]<siz[ry]) swap(rx,ry),swap(x,y);
    add(x,y),add(y,x);
    siz[rx]+=dfs(y,x);
}
int LCA(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=18;~i;i--)
        if(dep[f[x][i]]>=dep[y])
            x=f[x][i];
    if(x==y) return x;
    for(int i=18;~i;i--)
        if(f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][0];
}
int query(int rt1,int rt2,int rt3,int rt4,int l,int r,int k)
{
    if(l==r) return a[l];
    int mid=l+r>>1,s=sum[ch[rt1][0]]+sum[ch[rt2][0]]-sum[ch[rt3][0]]-sum[ch[rt4][0]];
    if(s>=k) return query(ch[rt1][0],ch[rt2][0],ch[rt3][0],ch[rt4][0],l,mid,k);
    else return query(ch[rt1][1],ch[rt2][1],ch[rt3][1],ch[rt4][1],mid+1,r,k-s);
}
int main()
{
    freopen("data.in","r",stdin);
    freopen("data.out","w",stdout);
    scanf("%d",&testcase);
    tot=0,cnt=0;
    scanf("%d%d%d",&n_,&m,&t);
    for(int i=1;i<=n_;i++) scanf("%d",a+i),b[i]=a[i];
    std::sort(a+1,a+1+n_);
    n=std::unique(a+1,a+1+n_)-a-1;
    for(int i=1;i<=n_;i++) b[i]=std::lower_bound(a+1,a+1+n,b[i])-a;
    for(int u,v,i=1;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    for(int i=1;i<=n_;i++)
        if(!f[i][0])
            siz[i]=dfs(i,0);
    int lastans=0;char op[4];
    for(int u,v,k,i=1;i<=t;i++)
    {
        scanf("%s%d%d",op,&u,&v);
        u^=lastans,v^=lastans;
        if(op[0]=='Q')
        {
            scanf("%d",&k);
            k^=lastans;int lca=LCA(u,v);
            printf("%d\n",lastans=query(root[u],root[v],root[lca],root[f[lca][0]],1,n,k));
        }
        else
            Merge(u,v);
    }
    return 0;
}

---

2018.9.4