斯坦福机器学习视频笔记 Week3 逻辑回归与正则化 Logistic Regression and Regularization

我们将讨论逻辑回归。 逻辑回归是一种将数据分类为离散结果的方法。 例如，我们可以使用逻辑回归将电子邮件分类为垃圾邮件或非垃圾邮件。 在本模块中，我们介绍分类的概念，逻辑回归的损失函数（cost functon），以及逻辑回归对多分类的应用。

我们还涉及正规化。 机器学习模型需要很好地推广到模型在实践中没有看到的新例子。 我们将介绍正则化，这有助于防止模型过度拟合训练数据。

Classification

分类问题其实和回归问题相似，不同的是分类问题需要预测的是一些离散值而不是连续值。

如垃圾邮件分类，信用卡欺诈，肿瘤诊断等等。离散值可以是任意可数多个。

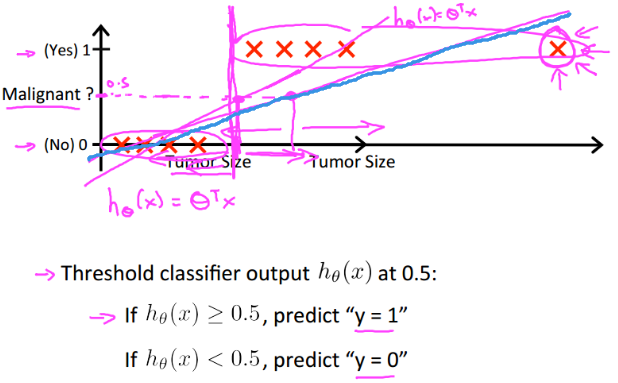
如果使用回归分析处理分类问题，如上图，当输出大于0.5时规定输出为1，小于0.5时输出为0，那么预测结果根据数据分布的不同会有很大误差。如那条蓝色的拟合直线。

而且预测值h(x)可以大于1或者小于0，这样回归方法将不好处理。

综上，我们引入 逻辑回归 使0<=h(x)<=1.

Hypothesis Representation

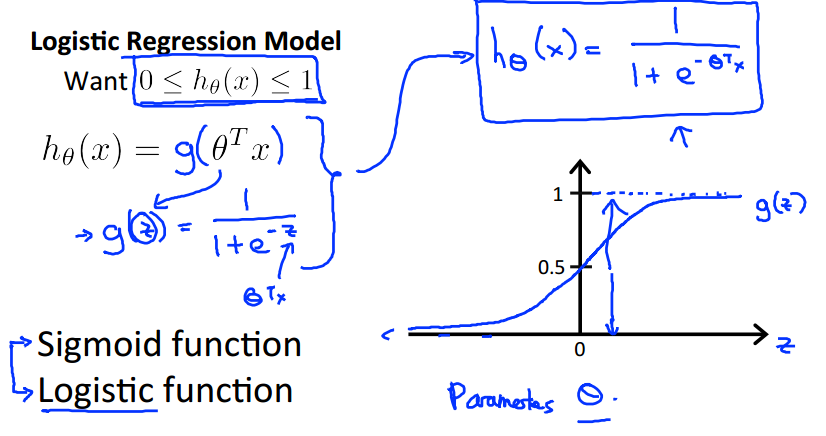
我们新引入的函数g（z）称为"Sigmoid Function,"或 "Logistic Function"，图像如上图。

逻辑函数g(z)可以将可以将任意的输入值限制在[0,1]之间的输出值。

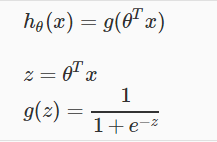
此时，hθ(x)的值表示输出结果为1时的概率。例如hθ(x) = 0.7表示输出为1的概率为0.7。同时表示，输出为0的概率为0.3

两个概率有如下关系：

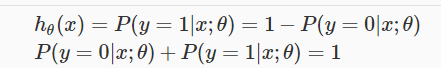
Decision Boundary

为了得到离散的分类值y = {0，1}，我们做如下处理：

当hθ(x)>=0.5时，输出1；当hθ(x)<0.5时，输出0.

当z>=0时，g(z)>=0.5;当z<0时，g(z)<0.5。

当输入变成theta*X时，有

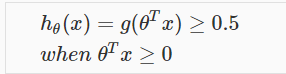
所以，我们最终得到：

这是我们想要的结果。

关于决策边界‘decision boundary’是将数据很好划分的一条分界线。

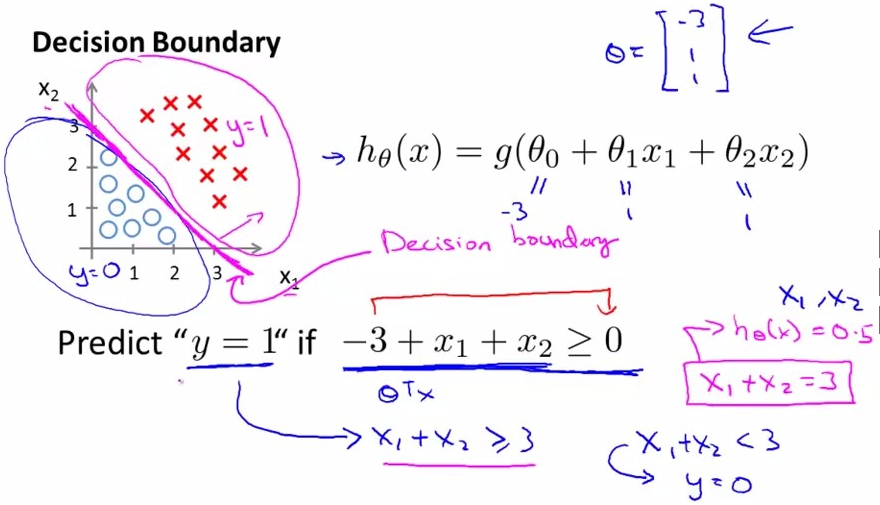
有如上图的数据分布，现在假设theta=[-3,1,1]T,带入到hθ(x)中，

假设现在要预测‘y=1’，使带入的结果-3+x1+x2 >0(之前的条件，z>=0),解除直线x1+x2=3便是数据集的分类边界。

另外一个例子可以看看：

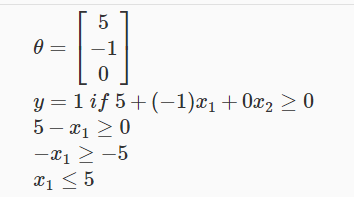
这里决策边界都是一条直线，而逻辑回归的决策边界其实可以是任何形状的，如下面：

Cost Function and Gradient Descent

我们不能在逻辑回归中使用和线性回归相同的cost function，因为其输出会是波动的，出现很多局部最小值，即它将不是‘凸函数’。

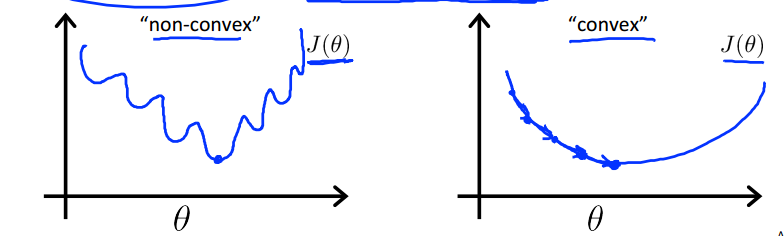
所以逻辑回归的损失函数定义如下：

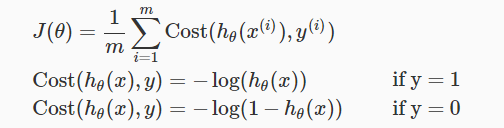
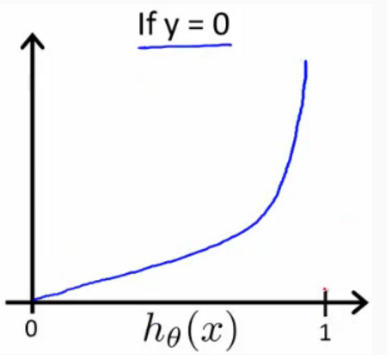
我们得到上面的 J(θ) vs hθ(x)的图像，

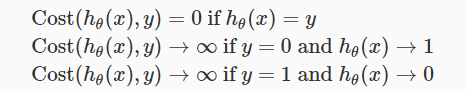
hθ(x) = 0时，Cost=0；y=0 && hθ(x)->1时，cost->∞。

现在的损失函数就是‘凸函数’了，这样我们就可以使用梯度下降算法来求解参数了。损失函数表达如下：

因为y={0,1},可以将J（theta）做如下简化：

然后就可以最小化J(theta)，求得参数theta。

使用梯度下降：

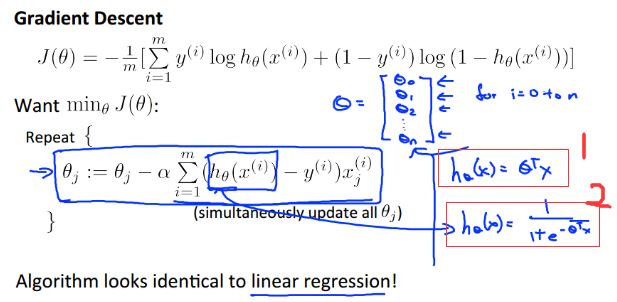
可以发现，这里的梯度下降迭代的式子和之前的线性回归在形式上是一样的，但是请注意，这里也就是在形式上相似而已，因为h(x)的表示都不同，上图中的1号框是线性回归的h(x),2号框是逻辑回归的h(x)表示的逻辑函数。

Advanced Optimization

这里讲的是关于Octive中使用高级优化的知识，这里仅仅附上两张ppt，详细的知识请去Coursera了解。

 function [jVal, gradient] = costFunction(theta)
   jVal = [...code to compute J(theta)...];
   gradient = [...code to compute derivative of J(theta)...];
 end

 options = optimset('GradObj', 'on', 'MaxIter', 100);
 initialTheta = zeros(2,1);
    [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

这部分联系在本周的编程联系上有涉及到。

Multiclass Classification: One-vs-all

现将逻辑回归应用到多元分类 y = {0,1...n}中。

上面所讲是一个三类型分类问题，基本思想是将n类的多元分类划分成n+1个二元分类问题，选择一个类为Positive，那么剩下的所有数据自动划分在对立的negative里。

在这里一共会有三个h(x)，分别对应3个不同类型的假设。

总结：

使用逻辑回归做多元分类，就是为每个类建立一个分类器h(x)，给出一个相应i类的y=i的概率。

如果要为新的输入值做预测，那么就选择n个分类器h(x)中有最大概率的那一个类作为预测值。

The Problem of Overfitting

下面是对同一个数据集采用的三种不同的拟合假设。

1. y = θ0+θ1x；

2. y=θ0+θ1x+θ2x^2;

3. 

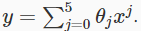
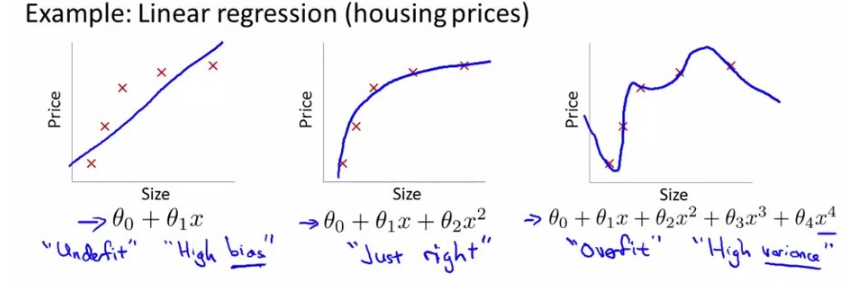
第一幅图显示的是 欠拟合(underfitting) 或者 高偏差(high bias)，指的是对数据趋势的拟合效果很差，当使用过于简单的拟合函数或使用过少的特征进行预测，会导致欠拟合；

第三幅图显示的是 过拟合(overfitting) 或者 高方差(high variance)，指的是对数据拟合很好，但是泛化能力(generalize)很差，也就是对新数据的预测能力很差，原因是使用了过于复杂的拟合函数。

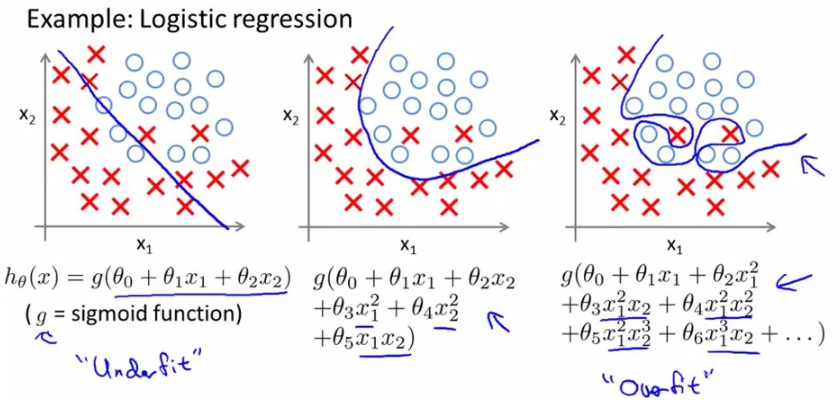
上面是关于逻辑回归的过拟合问题示例。

这里讲到有两种方法用于解决 过拟合 问题。

1）减少数据特征的数量

• 手动选择保留哪些特征；
• 使用模型选择算法（后面的课程会涉及到）；

2）正则化（Regularization）

• 保留所有的特征，减小参数theta的值；
• 当我们拥有很多不太有用的特征时，正则化会起到很好的作用；

Cost Function for Solving Overfitting

如果我们的假设函数有过拟合的问题，我们可以通过增加它们的成本cost，来减小我们的函数中的一些项的权重。

也就是说我们给某些theta值一个很大的惩罚项。如下面的例子，在theta3和theta4前面乘以1000的惩罚项，使theta3和theta4趋于0，以减小3次项和4次项对整个函数的影响，我们要使过拟合的函数接近于二次函数的图像。

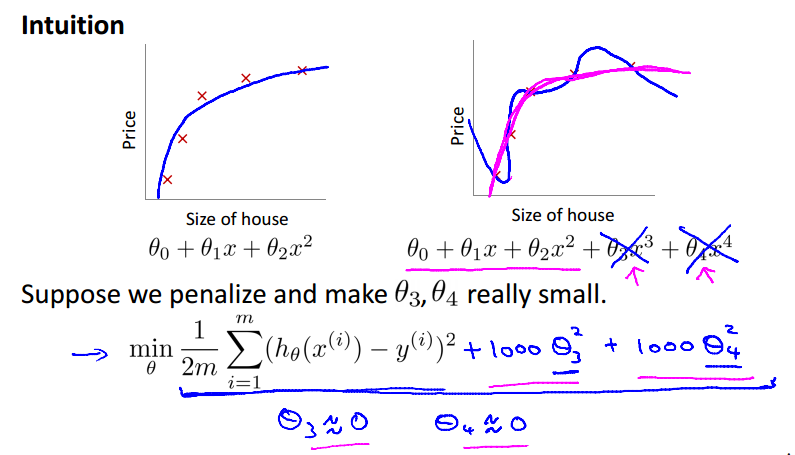
我们也可以‘惩罚’函数的每一项，使用下面的公式：

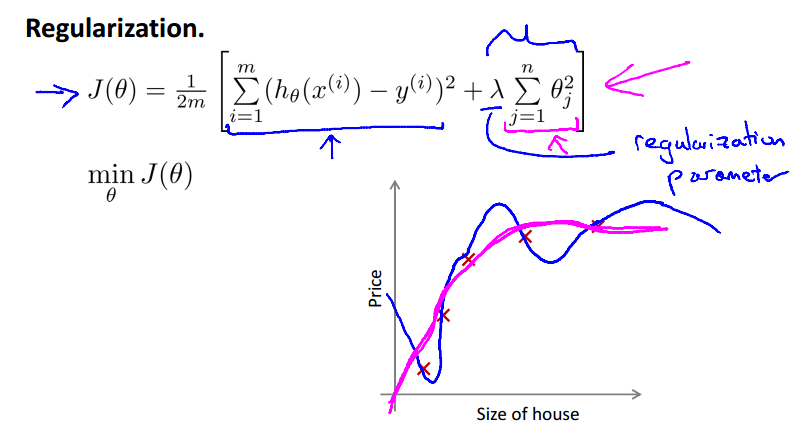
蓝色的图像是过拟合的图像，红色的项是正则化后的图像，显然后者对数据的拟合更好。惩罚项的参数lambda成为‘正则化参数’(regularization parameter)。

使用惩罚项，我们可以平滑函数曲线以减小过拟合。但如果lambda过大，会使theta->0，使数据 欠拟合，如下图。

相反，如果lambda过小，甚至直接为0，会导致 过拟合的情况。

Regularized Linear Regression

将正则化应用到线性回归中，下面是我们需要优化的 J(theta):

使用梯度下降算法：

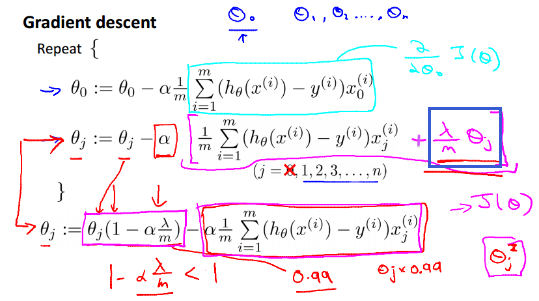
和之前的相比，正则化后的算法只是在 求theta时加了 一项λ/m×theta(蓝框中的项)，可以证明这是上面正则化后的J(theta)的求偏导的结果，从j=1开始。

注意，这里不需要惩罚theta0，所以把theta0的更新单列出来。

同样，正则化也可以在Normal Equation中使用，有以下公式。

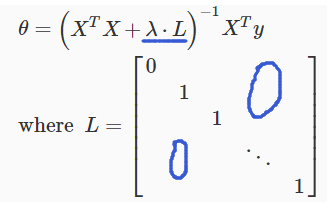
相比之前，我们只是添加了lambda*L这一项，其中矩阵L的形式如上所示。

回想，当m(example)<=n(feature)时，XT×X是不可逆的，但是添加lambda*L这一项后整体便是可逆的了。

Regularized Logistic Regression

我们同样可以将正则化应用到逻辑回归中，解决过拟合的问题。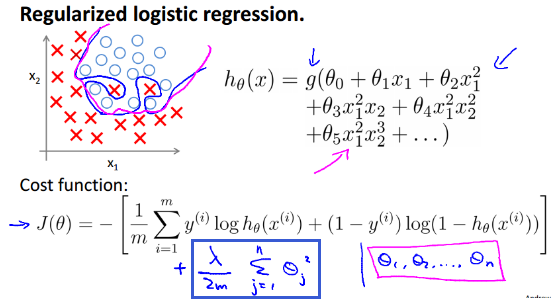

通过在损失函数加上蓝色方块中的惩罚项，便得到了正则化使用的J(theta),然后将其应用到梯度下降中：

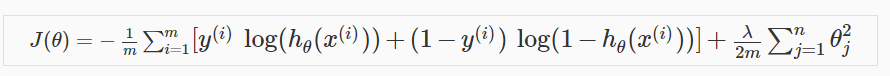
这里同样不需要惩罚theta0。

同样可以使用Octave提供的最优化方法实现正则化。

这样我们就解决了线性回归和逻辑回归中的过度拟合问题，小伙伴们赶紧去实现一下吧。