R: 主成分分析 ~ PCA(Principal Component Analysis)

本文摘自：http://www.cnblogs.com/longzhongren/p/4300593.html 以表感谢。感谢

综述： 主成分分析 因子分析 典型相关分析，三种方法的共同点主要是用来对数据降维处理。经过降维去除了噪声。

#主成分分析 是将多指标化为少数几个综合指标的一种统计分析方法。

是一种通过降维技术把多个变量化成少数几个主成分的方法，这些主成分能够反映原始变量的大部分信息，表示为原始变量的线性组合。

作用：1,解决自变量之间的多重共线性； 2,减少变量个数， 3,确保这些变量是相互独立的

应用场景：筛选回归变量 --> 回归分析

计算步骤：

假设样本观测数据矩阵为： X=(x1,x2,x3,...xp)，xi为n个样本在第i个属性上的观测值，是一个列向量

步1. 对原始数据标准化处理（0均值化处理），即每一维的数据都减去该维的均值。变换之后每一维的均值都变成了0。
步2. 计算样本相关系数矩阵。

　　

步3. 计算协方差矩阵的特征值和特征向量。对称方阵可求特征值、特征向量
步4. 选择重要的主成分，即大的特征值对应的特征向量，得到新的数据集。并写出主成分表达式。
步5. 计算主成分得分。
步6. 根据主成分得分的数据，做进一步的统计分析。

实例演示：

#原始数据：
dat <- data.frame(x=c(2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1),
                  y=c(2.4,0.7,2.9,2.2,3,2.7,1.6,1.1,1.6,0.9)); dat

#步1，数据标准化
dat1 <- scale(dat); dat1
#步2，求解协方差矩阵
covdat <- cov(dat1); covdat
#步3，求解特征值、特征向量
eigen_dat <- eigen(covdat); eigen_dat
#步4，求解主成分
dat1 %*% eigen_dat$vectors

 总和上述代码：

pca <- function(data = data){
  dat <- scale(data) #标准化
  covdat <- cov(dat)  #求协方差矩阵
  eigendat <- eigen(covdat)  #求特征值、特征向量
  eigenValue <- eigendat$values  #特征值
  eigenVector <- eigendat$vectors  #特征向量
  order_value <- order(eigenValue,decreasing = T)  #由大到小排列特征值
  values <- eigenValue[order_value]
  valueSum <- sum(values)
  cumVar <- cumsum(values)/valueSum * 100  #计算主成分得分。
  order_vector <- eigenVector[,order_value]
  principal <- dat %*% order_vector  #求解主成分
  return(list(PCA=principal, cumVar=cumVar))
}
pca(data=dat1)

R 中函数总结：

#R中作为主成分分析最主要的函数是 princomp() 函数
#princomp() 主成分分析   可以从相关阵或者从协方差阵做主成分分析
#summary() 提取主成分信息 
#loadings() 显示主成分分析或因子分析中载荷的内容
#predict() 预测主成分的值 
#screeplot() 画出主成分的碎石图 
#biplot() 画出数据关于主成分的散点图和原坐标在主成分下的方向

案例：

#现有30名中学生身高、体重、胸围、坐高数据，对身体的四项指标数据做主成分分析。

#1.载入原始数据
test<-data.frame(
  X1=c(148, 139, 160, 149, 159, 142, 153, 150, 151, 139,
           140, 161, 158, 140, 137, 152, 149, 145, 160, 156,
           151, 147, 157, 147, 157, 151, 144, 141, 139, 148),
  X2=c(41, 34, 49, 36, 45, 31, 43, 43, 42, 31,
           29, 47, 49, 33, 31, 35, 47, 35, 47, 44,
           42, 38, 39, 30, 48, 36, 36, 30, 32, 38),
  X3=c(72, 71, 77, 67, 80, 66, 76, 77, 77, 68,
          64, 78, 78, 67, 66, 73, 82, 70, 74, 78,
          73, 73, 68, 65, 80, 74, 68, 67, 68, 70),
  X4=c(78, 76, 86, 79, 86, 76, 83, 79, 80, 74,
           74, 84, 83, 77, 73, 79, 79, 77, 87, 85,
           82, 78, 80, 75, 88, 80, 76, 76, 73, 78)
  )

#2.作主成分分析并显示分析结果
test.pr<-princomp(test,cor=TRUE)   #cor是逻辑变量，cor=TRUE 表示用样本的相关矩阵R做主成分分析

若 cor=FALSE 表示用样本的协方差阵S做主成分分析
summary(test.pr,loadings=TRUE)  #loading是逻辑变量，当 loading=TRUE 时表示显示 loading 的内容

#loadings 的输出结果为载荷是主成分对应于原始变量的系数，即Q矩阵

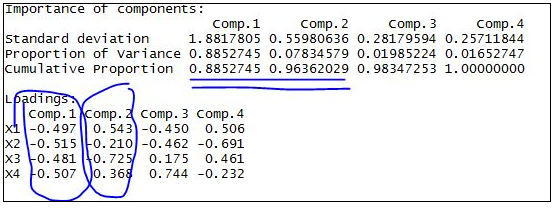
分析结果含义
#----Standard deviation 标准差   其平方为方差=特征值
#----Proportion of Variance  方差贡献率
#----Cumulative Proportion  方差累计贡献率

#由结果显示 前两个主成分的累计贡献率已经达到96% 可以舍去另外两个主成分 达到降维的目的

因此可以得到函数表达式 Z1=-0.497X'1-0.515X'2-0.481X'3-0.507X'4

Z2=  0.543X'1-0.210X'2-0.725X'3-0.368X'4

#4.画主成分的碎石图并预测

screeplot(test.pr,type="lines")

p <- predict(test.pr)

biplot(test.pr)  #画出数据关于主成分的散点图和原坐标在主成分下的方向

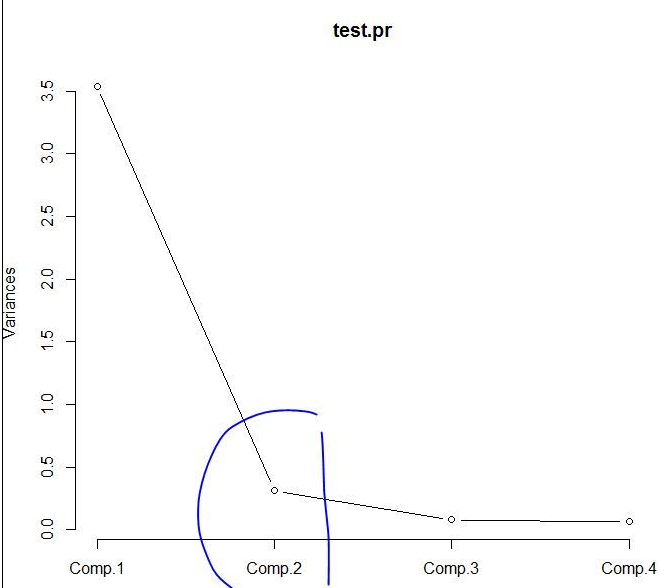
由碎石图可以看出 第二个主成分之后 图线变化趋于平稳 因此可以选择前两个主成分做分析。

扩展说明：

1，它是一个线性变换。这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。通常表示为原始变量的线性组合。

2，把多指标转化为少数几个综合指标，降低观测空间的维数，以获取最主要的信息。减少数据集的维数，同时保持数据集的对方差贡献最大的特征。

3，由主成分分析法构造回归模型。即把各主成分作为新自变量代替原来自变量 x 做回归分析。
4，用主成分分析筛选回归变量。回归变量的选择有着重的实际意义，为了使模型本身易于做结构分析、控制和预报，从原始变量所构成的子集合中选择最佳变量，构成最佳变量集合。用主成分分析筛选变量，可以用较少的计算量，获得选择最佳变量子集合的效果。