[算法模版]Link-Cut-Tree

[算法模版]Link-Cut-Tree

博主懒本博客只对现有博客进行补充，先直接放隔壁链接。

FlashHu-LCT总结

Menci-LCT学习笔记

基本思想

即“使用一个splay维护一条链，且这条链不存在在原树上的深度相同的点”。而这条链在splay中的存储方式是以节点在原树上的深度为关键字进行排序。（这也意味着这个splay的中序遍历和这条链在原树上的中序遍历是相同的，且这个中序遍历就是把这个链从浅到深写下来）

在push_up操作中这是个关键的性质。因为splay上的节点x的左子树就是他的一部分祖先节点，右子树就是他的一部分儿子节点。

makeroot操作

makeroot操作用于把任何一个点反转到当前树的根节点。

做法是先把要进行操作的节点x进行access，将root和x进行连通。然后进行splay(x)操作，把x变成splay的根。（请注意，这时候x在主树的深度仍然没有改变）。

随后将x的子树全部进行反转操作。也就是改变了这个splay的深度。虽然splay和splay之间的连接需要依赖深度关系（一棵splay的虚边连接向当前splay中序遍历序列的首位在原树上的父亲）。但是因为相对关系不变，所以不影响。

看图（图来自 动态仙人掌系列题解之四）：

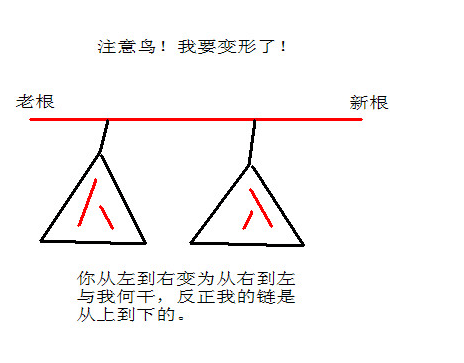
可以把连接老根和新根的splay看作一个无法弯曲的杆子，其他splay都是连接在杆子上的块。旋转操作虽然会改变杆子上每一点的深度，但是却不会改变块和杆子上连接点的相对深度关系。所以不会这样变换老根和新根不会对树的结构造成破坏。

另外如果维护的值是和树的形态相关的，这样使用makeroot很可能就会出锅（比如 SP2939 QTREE5 - Query on a tree V）。那么makeroott就不能使用了。因为涉及makeroot的操作有link,cut,split。我们得想办法解决这个问题：

• Link之所以需要在link中makeroot(x)，是因为根据定义，对于一条虚边u,v，在原树上是一条连接u,root[v]的边（这里root[]是splay的root）。所以我们需要保证连接的其中一个端点f[x]=0且root[x]=x即可。

findroot操作

因为已经makeroot(x)了，所以x一定是最浅的点。我们必须要保证三个条件才能cut:

1. 在同一棵树。
2. y的父亲是x。
3. y没有左子树。

后两个条件保证了x和y在原树上是直接连接的。

代码

洛谷3690

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define maxn (int)(3e5+1000)
int f[maxn],v[maxn],s[maxn],st[maxn],c[maxn][2];
bool r[maxn];
using namespace std;
int n,m;
void pushr(int x){
    swap(c[x][0],c[x][1]);r[x]^=1;
}
void pushdown(int x){
    if(!r[x])return;
    if(c[x][0])pushr(c[x][0]);
    if(c[x][1])pushr(c[x][1]);
    r[x]=0;
}
void pushup(int x){
    s[x]=s[c[x][0]]^s[c[x][1]]^v[x];
}

bool nroot(int x){
    return c[f[x]][0]==x||c[f[x]][1]==x;
}
void rotate(int x){
    int y=f[x],z=f[y],k=(c[y][1]==x),w=c[x][!k];
    bool flag=nroot(y);

    c[y][k]=c[x][!k];
    f[c[x][!k]]=y;

    c[x][!k]=y;
    f[y]=x;

    if(flag)c[z][c[z][1]==y]=x;
    f[x]=z;
    pushup(y);
    pushup(x);
}
void splay(int x){
    int y=x,z=0;
    st[++z]=y;
    while(nroot(y))st[++z]=y=f[y];
    while(z)pushdown(st[z--]);
    for(;nroot(x);rotate(x)){
        y=f[x];
        if(!nroot(f[x]))continue;
        rotate((c[f[x]][0]==x)==(c[f[y]][0]==y)?y:x);
    }
  //  pushup(x);
}
void access(int x){
    for(int y=0;x;y=x,x=f[x]){
        splay(x);c[x][1]=y;pushup(x);
    }
}
int findroot(int x){
    access(x);splay(x);
    while(c[x][0]){
        x=c[x][0];
        pushdown(x);
    }
    splay(x);
    return x;
}
void makeroot(int x){
    access(x);splay(x);pushr(x);
}
void split(int x,int y){
    makeroot(x);access(y);splay(y);
}
void link(int x,int y){

    if(findroot(x)!=findroot(y)){makeroot(x);f[x]=y;}
}
void cut(int x,int y){
    makeroot(x);
    if(findroot(y)==x&&f[y]==x&&!c[y][0]){
        f[y]=c[x][1]=0;
        pushup(x);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&v[i]);
    for(int i=1;i<=m;i++){
        int ty,x,y;scanf("%d%d%d",&ty,&x,&y);
        if(ty==0){
            split(x,y);
            printf("%d\n",s[y]);
        }
        else if(ty==1){
            link(x,y);
        }
        else if(ty==2){
            cut(x,y);
        }
        else if(ty==3){
            splay(x);v[x]=y;//pushup(x);
        }
    }
}

易错点

• 调用access(x)后，x所在splay的根可能不是x，也可能不是原树的根。所以在查询某条路径\(u,v\)的答案时，一定需要在makeroot(x),access(y)之后必须加上splay(x)或splay(y)，才能保证x或y在splay的根上。
• findroot时应该先pushdown再判断左儿子是不是0，然后才能向左儿子走（因为可能左儿子原来不是0，pushdown之后变成了0，这时候走左儿子就会炸掉）。所以应该写成：while(c[x][0])x=c[x][0],push_down(x);
• cut中判断条件合法会进行findroot(y)，但是findroot(y)末尾如果没有对查询结果执行splay()就会锅掉。因为cut中会先makeroot(x)，findroot(y)如果查询之后不把结果splay上去那么根就不是x了，接着cut就会出锅。