GBDT（梯度提升树） 原理小结

　　　　在之前博客中，我们对Boosting家族的Adaboost算法做了总结，本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boosting Decison Tree, 以下简称GBDT)做一个总结。GBDT有很多简称，有GBT（Gradient Boosting Tree）, GTB（Gradient Tree Boosting ）， GBRT（Gradient Boosting Regression Tree）, MART(Multiple Additive Regression Tree)，其实都是指的同一种算法，本文统一简称GBDT。GBDT在BAT大厂中也有广泛的应用，假如要选择3个最重要的机器学习算法的话，个人认为GBDT应该占一席之地。

1. GBDT概述

　　　　GBDT也是集成学习Boosting家族的成员，但是却和传统的Adaboost有很大的不同。回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。

　　　　在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是ft-1(x)损失函数是L(y,ft-1(x)) 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器ht(x)，让本轮的损失L(t,ft-1(x)+ht(x))最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。

　　　　GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

　　　　从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？

2. GBDT的负梯度拟合

　　　　在上一节中，我们介绍了GBDT的基本思路，但是没有解决损失函数拟合方法的问题。针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为:

　　 

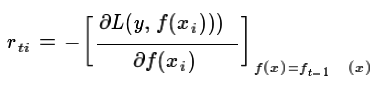
　　　　利用(xi,rti)(i=1,2,...m),我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域Rtj,j=1,2,...,J。其中J为叶子节点的个数。

　　　　针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值ctj如下：

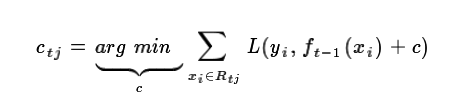
　　　　这样我们就得到了本轮的决策树拟合函数如下：

　　　　从而本轮最终得到的强学习器的表达式如下：

　　　　通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无轮是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。

3. GBDT回归算法

　　　　好了，有了上面的思路，下面我们总结下GBDT的回归算法。为什么没有加上分类算法一起？那是因为分类算法的输出是不连续的类别值，需要一些处理才能使用负梯度，我们在下一节讲。

　　　　输入:是训练集样本T={(x1,y1),(x2,y2)...(xm,ym)}， 最大迭代次数T, 损失函数L。

输出是强学习器f(x)

　　　　1) 初始化弱学习器:

　　

　　　　

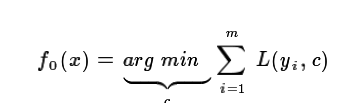
　　　　2) 对迭代轮数t=1,2,...T有：

　　　　　　a)对样本i=1,2，...m，计算负梯度

　　   

　　　　　　b)利用(xi,r ti)(i=1,2...m), 拟合一颗CART回归树,得到第t颗回归树，其对应的叶子节点区域为Rtj,j=1.2...J 。其中J为回归树t的叶子节点的个数。

　　　　　　c) 对叶子区域j =1,2,..J,计算最佳拟合值

　　　

　　　　　　 d) 更新强学习器

　　　

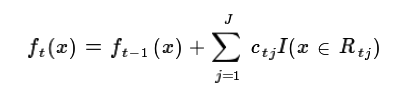
　　　　3) 得到强学习器f(x)的表达式

　　　

4. GBDT分类算法

　　　　这里我们再看看GBDT分类算法，GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

　　　　为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。

4.1 二元GBDT分类算法

　　　　对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为：

　　

　　　　其中y {-1,1} 则此时的负梯度误差为:

　　

　　　　对于生成的决策树，我们各个叶子节点的最佳残差拟合值为:

　　

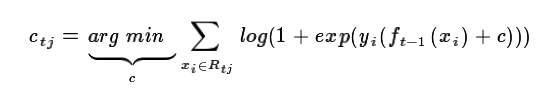
　　　　由于上式比较难优化，我们一般使用近似值代替

　　　

　　　　除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。

4.2 多元GBDT分类算法

　　　　多元GBDT要比二元GBDT复杂一些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为：

　

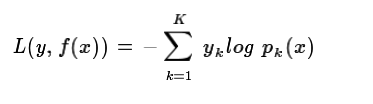
　　　　其中如果样本输出类别为k，则yk=1第k类的概率Pk(x)表达式为：

　　　

　　　　集合上两式，我们可以计算出第t轮的i个样本对应类别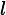 的负梯度误差为:

　　　

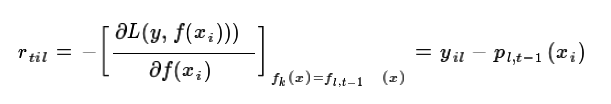
　　　　观察上式可以看出，其实这里的误差就是样本i对应类别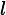 的真实概率和t-1轮预测概率的差值。

　　　　对于生成的决策树，我们各个叶子节点的最佳残差拟合值为:

　　　

　　　　由于上式比较难优化，我们一般使用近似值代替：

　　　

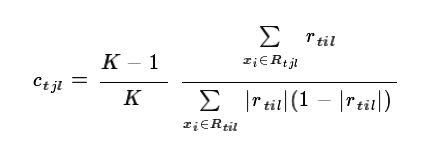
　　　　除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。

5. GBDT常用损失函数

　　　　这里我们再对常用的GBDT损失函数做一个总结。

　　　　对于分类算法，其损失函数一般有对数损失函数和指数损失函数两种:

　　　　a) 如果是指数损失函数，则损失函数表达式为

　　　

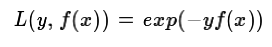
　　　　　其负梯度计算和叶子节点的最佳残差拟合参见Adaboost原理篇。

　　　　b) 如果是对数损失函数，分为二元分类和多元分类两种，参见4.1节和4.2节。

　　　　对于回归算法，常用损失函数有如下4种:

　　　　a)均方差，这个是最常见的回归损失函数了

　　

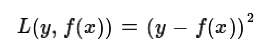
　　　　b)绝对损失，这个损失函数也很常见

　　

　　　　对应负梯度误差为：

　

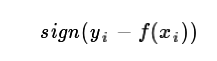
　　　　c)Huber损失，它是均方差和绝对损失的折衷产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下：　　

　　

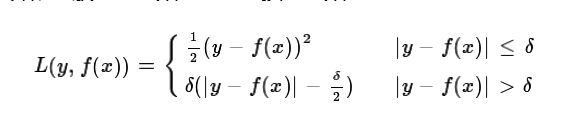
　　　　　对应的负梯度误差为：

　　

　　　　d) 分位数损失。它对应的是分位数回归的损失函数，表达式为

　

　　　　　　其中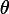 为分位数，需要我们在回归前指定。对应的负梯度误差为：

　

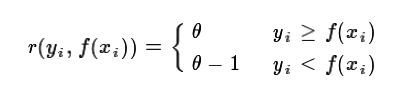
　　　　　　对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。

6. GBDT的正则化

　　　　和Adaboost一样，我们也需要对GBDT进行正则化，防止过拟合。GBDT的正则化主要有三种方式。

　　　　第一种是和Adaboost类似的正则化项，即步长(learning rate)。定义为V，对于前面的弱学习器的迭代

　　

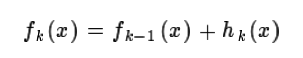
　　　　如果我们加上了正则化项，则有:

　　

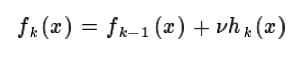
　　　    v 的取值范围为0<v<1.对于同样的训练集学习效果，较小的v意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

　　　　第二种正则化的方式是通过子采样比例（subsample）。取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。

　　　　使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。

　　　　第三种是对于弱学习器即CART回归树进行正则化剪枝。在决策树原理篇里我们已经讲过，这里就不重复了。

7. GBDT小结　

　　　　GBDT终于讲完了，GDBT本身并不复杂，不过要吃透的话需要对集成学习的原理，决策树原理和各种损失函树有一定的了解。由于GBDT的卓越性能，只要是研究机器学习都应该掌握这个算法，包括背后的原理和应用调参方法。目前GBDT的算法比较好的库是xgboost。当然scikit-learn也可以。

　　　　最后总结下GBDT的优缺点。

　　　　GBDT主要的优点有：

　　　　1) 可以灵活处理各种类型的数据，包括连续值和离散值。

　　　　2) 在相对少的调参时间情况下，预测的准确率也可以比较高。这个是相对SVM来说的。

　　　　3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

　　　　GBDT的主要缺点有：

　　　　1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

          （文章参考自刘建平机器学习）