003-结构型-06-组合模式（Composite）

一、概述

　　将对象组合成树形结构以表示“部分一整体”的层次结构

　　组合模式是为了表示那些层次结构，同时部分和整体也可能是一样的结构，常见的如文件夹或者树。

　　通过递归手段来构造树形的对象结构，并可以通过一个对象来访问整个对象树。

　　组合(Composite)模式的其它翻译名称也很多，比如合成模式、树模式等等。在《设计模式》一书中给出的定义是：将对象以树形结构组织起来，以达成“部分－整体”的层次结构，使得客户端对单个对象和组合对象的使用具有一致性。

1.1、适用场景

　　希望客户端可以忽略组合对象与单个对象的差异时

　　处理一个树形结构时

1.2、优缺点

优点：

• 清楚地定义分层次的复杂对象，表示对象的全部或部分层次
• 让客户端忽略了层次的差异，方便对整个层次结构进行控制
• 简化客户端代码
• 符合开闭原则

缺点：

• 限制类型时会较为复杂
• 使设计变得更加抽象
• 组合模式不容易限制组合中的构件

1.3、类图角色及其职责

　　

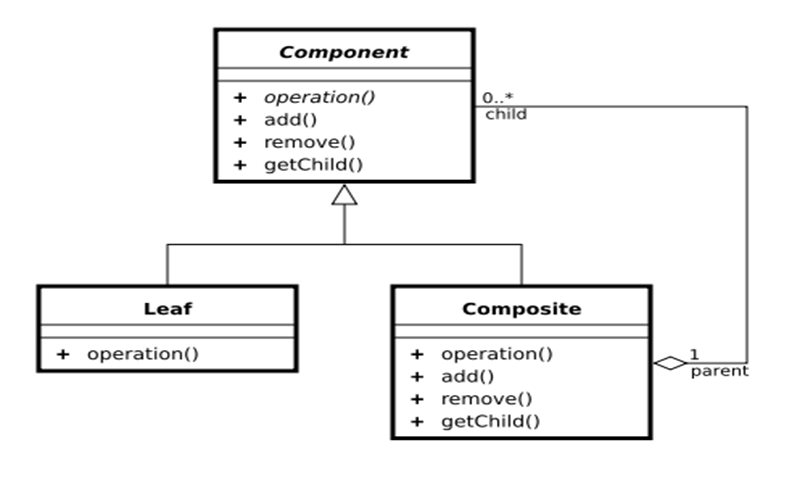
组合模式的角色和职责

　　1、Component （树形结构的节点抽象）

　　　　1.1、为所有的对象定义统一的接口（公共属性，行为等的定义）

　　　　1.2、提供管理子节点对象的接口方法

　　　　1.3、[可选]提供管理父节点对象的接口方法

　　2、Leaf （树形结构的叶节点）

　　　　Component的实现子类

　　3、Composite（树形结构的枝节点）

　　　　Component的实现子类

　　安全性与透明性

　　组合模式中必须提供对子对象的管理方法，不然无法完成对子对象的添加删除等等操作，也就失去了灵活性和扩展性。但是管理方法是在Component中就声明还是在Composite中声明呢？

　　一种方式是在Component里面声明所有的用来管理子类对象的方法，以达到Component接口的最大化（如下图所示）。目的就是为了使客户看来在接口层次上树叶和分支没有区别——透明性。但树叶是不存在子类的，因此Component声明的一些方法对于树叶来说是不适用的。这样也就带来了一些安全性问题。

　　　　

　　另一种方式就是只在Composite里面声明所有的用来管理子类对象的方法（如下图所示）。这样就避免了上一种方式的安全性问题，但是由于叶子和分支有不同的接口，所以又失去了透明性。

　　　　

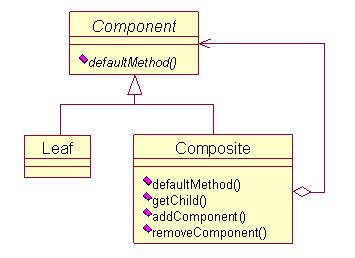
　　《设计模式》一书认为：在这一模式中，相对于安全性，我们比较强调透明性。对于第一种方式中叶子节点内不需要的方法可以使用空处理或者异常报告的方式来解决。

1.4、演进过程

示例、文件夹与文件，层次结构就符合树形结构

项目代码：https://github.com/bjlhx15/patterns.git 中的patterns-base 中 structure/composite

二、扩展

2.1 jdk

• java.awt.Container、Component
• java.util.HashMap、
• java.util.ArrayList、List、Collection

2.2 Mybatis

org.apache.ibatis.scripting.xmltags.SqlNode

MixedSqlNode相当于CourseCatalog课程目录

分隔