codeforces 260 div2 A,B,C

A:水的问题。排序结构。看看是否相同两个数组序列。

B：他们写出来1，2，3，4，的n钍对5余。你会发现和5环节。

假设%4 = 0，输出4，否则输出0.

写一个大数取余就过了。

B. Fedya and Maths

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Fedya studies in a gymnasium. Fedya's maths hometask is to calculate the following expression:

(1n + 2n + 3n + 4n) mod 5

for given value of n. Fedya managed to complete the task. Can you? Note that given number n can
be extremely large (e.g. it can exceed any integer type of your programming language).

Input

The single line contains a single integer n (0 ≤ n ≤ 10105).
The number doesn't contain any leading zeroes.

Output

Print the value of the expression without leading zeros.

Sample test(s)

input

4

output

4

input

124356983594583453458888889

output

0

Note

Operation x mod y means taking remainder after division x by y.

Note to the first sample:

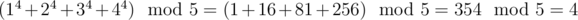
#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
///#define LL __int64
#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)

using namespace std;

const int maxn = 1000010;

int main()
{
    string s;
    while(cin >>s)
    {
        int n= s.size();
        int cnt = s[0]-'0';
        for(int i = 1; i < n; i++)
        {
            cnt %= 4;
            cnt = (cnt*10+(s[i]-'0'))%4;
        }
        if(cnt%4 == 0)
            cout<<4<<endl;
        else cout<<0<<endl;
    }
}

C：给你一些数。你取了一个数那么比这个数大1，和小1的数字就会被删掉。

问你最大能取到的数的和。

先依据数字进行哈希，然后线性的dp一遍，dp[i][1] = ma(dp[i-2][0], dp[i-2][1]) + vis[i]*i,dp[i][0] = max(dp[i-1][0], dp[i-1][1]).1代表取这个数。0代表不取。注意数据类型要用long long。

C. Boredom

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Alex doesn't like boredom. That's why whenever he gets bored, he comes up with games. One long winter evening he came up with a game and decided to play it.

Given a sequence a consisting of n integers. The
player can make several steps. In a single step he can choose an element of the sequence (let's denote it ak)
and delete it, at that all elements equal to ak + 1 and ak - 1 also
must be deleted from the sequence. That step brings ak points
to the player.

Alex is a perfectionist, so he decided to get as many points as possible. Help him.

Input

The first line contains integer n (1 ≤ n ≤ 105)
that shows how many numbers are in Alex's sequence.

The second line contains n integers a1, a2,
..., an (1 ≤ ai ≤ 105).

Output

Print a single integer — the maximum number of points that Alex can earn.

Sample test(s)

input

2
1 2

output

2

input

3
1 2 3

output

4

input

9
1 2 1 3 2 2 2 2 3

output

10

Note

Consider the third test example. At first step we need to choose any element equal to 2. After that step our sequence looks like this [2, 2, 2, 2].
Then we do 4 steps, on each step we choose any element equals to 2.
In total we earn 10 points.

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
///#define LL __int64
#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?

0:x)

using namespace std;

const int maxn = 1000010;

LL vis[maxn];
LL dp[maxn][2];

int main()
{
    int n;
    while(cin >>n)
    {
        int x;
        memset(vis, 0, sizeof(vis));
        memset(dp, 0, sizeof(dp));
        for(int i = 0; i < n; i++)
        {
            scanf("%d",&x);
            vis[x] ++;
        }
        dp[1][1] = vis[1];
        dp[2][1] = vis[2]*2;
        dp[2][0] = dp[1][1];
        for(int i = 3; i <= maxn-10; i++)
        {
            dp[i][1] = max(dp[i-2][0], dp[i-2][1])+vis[i]*i;
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
        }
        cout<<max(dp[maxn-10][0], dp[maxn-10][1])<<endl;
    }
    return 0;
}

版权声明：本文博主原创文章，博客，未经同意不得转载。