BZOJ2539 Spoj 10707 Count on a tree II

题面

题解

因为这道题目我也不太会做，所以借鉴了一下大佬heyujun的博客

---

如果不强制在线，这道题目是树上莫队练手题

我们知道莫队是离线的，但是万一强制在线就凉凉了

于是我们就需要一些操作：树分块

看到这个图：

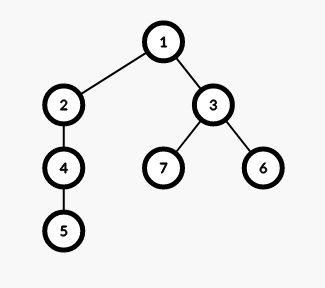
这里有\(7\)个点，我们每隔\(2\)深度分块

但是我们要保证分块的连续性，于是分成了\((1,2)(7,6,3)(4,5)\)三块

现在给了你两个将询问的点\(u,v(dep[u]>dep[v])\)，分类讨论：

1. 两个点在同一个块内

   直接暴力

2. 两个点不在同一个块内

   这种情况比较复杂，记一个块的根为\(rt[i]\)，则它到另外所有点的答案我们可以很轻松地
   
   统计出来，只需要对于每个\(rt[i]\)暴力统计一遍就可以了。

   那么现在我们要考虑的只有\(u\)到它的块的根\(x\)路径上是否会对答案产生贡献：
   
   对于这个，我们可以将这个分块可持久化，维护这个点的颜色在它的祖先中出现最深的位置
   
   的深度，那么一个块只需继承上面的块，并将在这个块中颜色的答案更新，因为那个颜色如
   
   果出现在这个位置，那么答案肯定更优。

   有了上面的铺垫，那我们只需对\(u\to x\)上的点暴力算它的深度是否超过\(\mathrm{LCA}(u, v)\)即可

代码

#include<cstdio>
#include<cstring>
#include<cctype>
#include<cmath>
#include<algorithm>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define clear(x, y) memset(x, y, sizeof(x))

inline int read()
{
	int data = 0, w = 1; char ch = getchar();
	while(ch != '-' && (!isdigit(ch))) ch = getchar();
	if(ch == '-') w = -1, ch = getchar();
	while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

const int maxn(40010), SQRT(210);
struct edge { int next, to; } e[maxn << 1];
int head[maxn], e_num;
inline void add_edge(int from, int to)
{
	e[++e_num] = (edge) {head[from], to};
	head[from] = e_num;
}

int n, m, Len, a[maxn], b[maxn], _a[maxn], r[maxn];
int P[maxn][SQRT], A[SQRT][maxn], fa[maxn], dep[maxn];
int q[maxn], belong[maxn], top, cnt, SIZE, root[maxn];
int c[maxn], Ans;

struct Block
{
	int a[SQRT]; void insert(const Block&, int, int);
	int &operator [] (const int &x) { return P[a[b[x]]][r[x]]; }
	const int &operator [] (const int &x) const { return P[a[b[x]]][r[x]]; }
} s[maxn];

void Block::insert(const Block &rhs, int x, int d)
{
	int blk = b[x], t = r[x];
	memcpy(a, rhs.a, sizeof(a));
	memcpy(P[++SIZE], P[a[blk]], sizeof(P[0]));
	P[a[blk] = SIZE][t] = d;
}

namespace Tree
{
	int belong[maxn], heavy[maxn], size[maxn];
	void dfs(int x, int chain)
	{
		belong[x] = chain;
		if(!heavy[x]) return;
		dfs(heavy[x], chain);
		for(RG int i = head[x]; i; i = e[i].next)
		{
			int to = e[i].to;
			if(to == fa[x] || to == heavy[x]) continue;
			dfs(to, to);
		}
	}

	int LCA(int x, int y)
	{
		while(belong[x] != belong[y])
		{
			if(x[belong][dep] < y[belong][dep]) std::swap(x, y);
			x = x[belong][fa];
		}
		return dep[x] < dep[y] ? x : y;
	}
}

int dfs(int x, int f)
{
	using Tree::size; using Tree::heavy;
	fa[x] = f, size[x] = 1;
	s[x].insert(s[f], a[x], dep[x] = dep[f] + 1);
	q[++top] = x; int maxd = dep[x], p = top;
	for(RG int i = head[x]; i; i = e[i].next)
	{
		int to = e[i].to; if(to == f) continue;
		maxd = std::max(maxd, dfs(to, x)); size[x] += size[to];
		if(size[heavy[x]] < size[to]) heavy[x] = to;
	}

	if(maxd - dep[x] >= Len || p == 1)
	{
		root[++cnt] = x;
		for(RG int i = p; i <= top; i++) belong[q[i]] = cnt;
		top = p - 1; return dep[x] - 1;
	}
	return maxd;
}

void Pre(int x, int f, int *s)
{
	if(!c[a[x]]++) ++Ans; s[x] = Ans;
	for(RG int i = head[x]; i; i = e[i].next) if(e[i].to != f)
		Pre(e[i].to, x, s);
	if(!--c[a[x]]) --Ans;
}

int Solve1(int x, int y)
{
	for(top = Ans = 0; x != y; x = fa[x])
	{
		if(dep[x] < dep[y]) std::swap(x, y);
		if(!c[q[++top] = a[x]]) c[a[x]] = 1, ++Ans;
	}
	for(Ans += !c[a[x]]; top;) c[q[top--]] = 0;
	return Ans;
}

int Solve2(int x, int y)
{
	if(dep[root[belong[x]]] < dep[root[belong[y]]]) std::swap(x, y);
	int x1 = root[belong[x]], d = dep[Tree::LCA(x, y)]; Ans = A[belong[x]][y];
	for(top = 0; x != x1; x = fa[x])
		if(!c[a[x]] && s[x1][a[x]] < d && s[y][a[x]] < d)
			c[q[++top] = a[x]] = 1, ++Ans;
	while(top) c[q[top--]] = 0;
	return Ans;
}

int main()
{
#ifndef ONLINE_JUDGE
	freopen("cpp.in", "r", stdin);
#endif
	n = read(), m = read(), Len = sqrt(n) - 1;
	for(RG int i = 1; i <= n; i++) b[i] = (i - 1) / Len + 1, r[i] = i % Len;
	for(RG int i = 1; i <= n; i++) a[i] = _a[i] = read();
	std::sort(_a + 1, _a + n + 1);
	int tot = std::unique(_a + 1, _a + n + 1) - _a - 1;
	for(RG int i = 1; i <= n; i++)
		a[i] = std::lower_bound(_a + 1, _a + tot + 1, a[i]) - _a;
	for(RG int i = 1, x, y; i < n; i++) x = read(), y = read(),
		add_edge(x, y), add_edge(y, x);
	top = 0, dfs(1, 0), Tree::dfs(1, 1);
	for(RG int i = 1; i <= cnt; i++) Pre(root[i], 0, A[i]);
	int ans = 0; while(m--)
	{
		int x = ans ^ read(), y = read();
		printf("%d\n", ans = (belong[x] == belong[y] ?
					Solve1(x, y) : Solve2(x, y)));
	}
	return 0;
}