bzoj4399 魔法少女LJJ 线段树合并

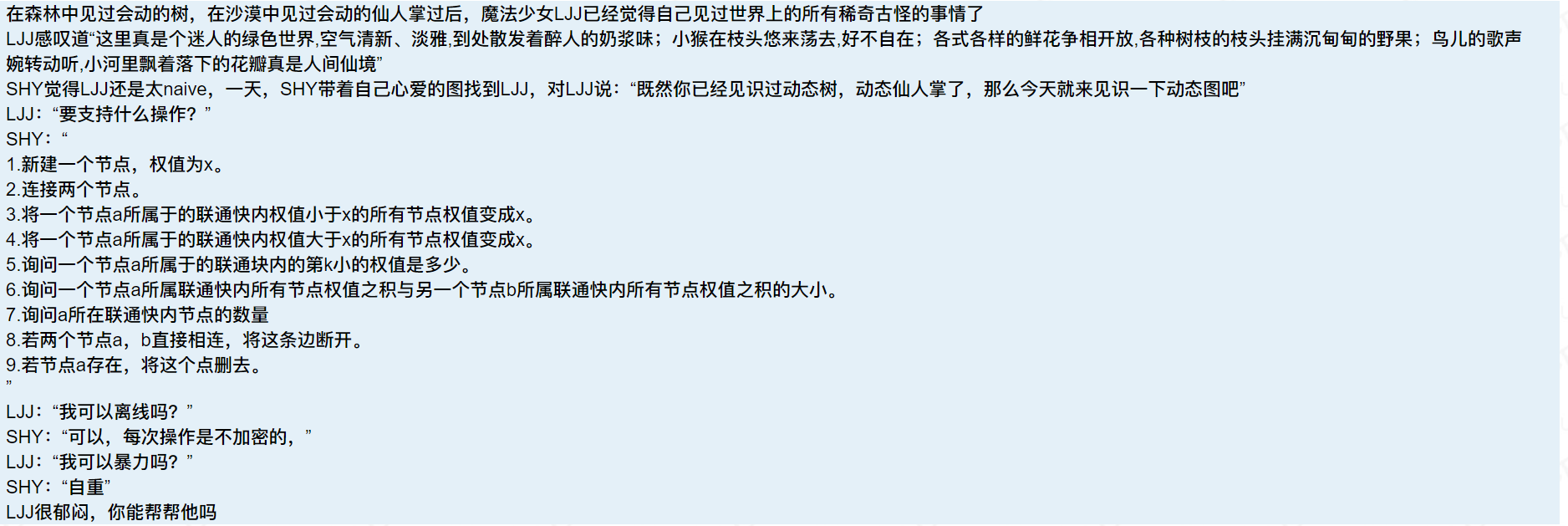
只看题面绝对做不出系列....

---

注意到\(c \leqslant 7\)，因此不会有删边操作（那样例删边干嘛）

注意到\(2, 5\)操作十分的有趣，启示我们拿线段树合并来做

操作\(7\)很好处理

操作\(6\)，维护对数的和即可

操作\(3, 4\)，乍看不好处理，然而势能分析一下就可以得出暴力的复杂度是\(O(n \log n)\)的

然而我好像写了个稳定的\(\log\)维护

然后好像就没了诶......

空间直接动态开点是开不下的....

需要预先离散化权值

复杂度\(O(n \log n)\)

---

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

#define de double
#define ri register int
#define rep(io, st, ed) for(ri io = st; io <= ed; io ++)

#define gc getchar
inline int read() {
	int p = 0, w = 1; char c = gc();
	while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); }
	while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc();
	return p * w;
}

const int sid = 5e5 + 5;
const int eid = 5e6 + 5;

de mul[eid];
int n, m, id, nc;
int rt[sid], fa[sid];
int ls[eid], rs[eid], sz[eid];
int opt[sid], c1[sid], c2[sid], T[sid];

inline int find(int o) { return fa[o] = (o == fa[o]) ? o : find(fa[o]); }

inline void upd(int o) {
	int lc = ls[o], rc = rs[o];
	sz[o] = sz[lc] + sz[rc];
	mul[o] = mul[lc] + mul[rc];
}

inline int merge(int x, int y) {
	if(!x || !y) return x + y;
	ls[x] = merge(ls[x], ls[y]);
	rs[x] = merge(rs[x], rs[y]);
	sz[x] = sz[x] + sz[y];
	mul[x] = mul[x] + mul[y];
	return x;
}

inline void mdf(int &o, int l, int r, int c, int v) {
	if(!o) o = ++ id;
	if(l == r) { sz[o] = v; mul[o] = (de)v * (de)log(T[c]); return; }
	int mid = (l + r) >> 1;
	if(c <= mid) mdf(ls[o], l, mid, c, v);
	else mdf(rs[o], mid + 1, r, c, v);
	upd(o);
}

inline int dfs(int &o, int l, int r, int ml, int mr) {
	if(!o || ml > r || mr < l) return 0;
	if(ml <= l && mr >= r) {
		int tmp = sz[o]; o = 0;
		return tmp;
	}
	int mid = (l + r) >> 1;
	int ret = dfs(ls[o], l, mid, ml, mr) + dfs(rs[o], mid + 1, r, ml, mr);
	upd(o); return ret;
}

inline int qry(int o, int l, int r, int k) {
	if(l == r) return T[l];
	int mid = (l + r) >> 1;
	if(sz[ls[o]] >= k) return qry(ls[o], l, mid, k);
	else return qry(rs[o], mid + 1, r, k - sz[ls[o]]);
}

void calc() {
	rep(i, 1, m) {
		opt[i] = read(); c1[i] = read();
		if(opt[i] != 1 && opt[i] != 7) c2[i] = read();
		if(opt[i] == 1) T[++ nc] = c1[i];
		if(opt[i] == 3 || opt[i] == 4) T[++ nc] = c2[i];
	}

	sort(T + 1, T + nc + 1);
	nc = unique(T + 1, T + nc + 1) - T - 1;
	rep(i, 1, m) {
		if(opt[i] == 1)
			c1[i] = lower_bound(T + 1, T + nc + 1, c1[i]) - T;
		if(opt[i] == 3 || opt[i] == 4)
			c2[i] = lower_bound(T + 1, T + nc + 1, c2[i]) - T;
	}

	rep(i, 1, m) {
		int u, v, w, num;
		switch(opt[i]) {
			case 1 :
				n ++; fa[n] = n;
				mdf(rt[n], 1, nc, c1[i], 1); break;
			case 2 :
				u = find(c1[i]); v = find(c2[i]);
				if(u == v) break;
				fa[v] = u; rt[u] = merge(rt[u], rt[v]); break;
			case 3 :
				u = find(c1[i]); w = c2[i];
				num = dfs(rt[u], 1, nc, 1, w);
				mdf(rt[u], 1, nc, w, num); break;
			case 4 :
				u = find(c1[i]); w = c2[i];
				num = dfs(rt[u], 1, nc, w, nc);
				mdf(rt[u], 1, nc, w, num); break;
			case 5 :
				u = find(c1[i]); w = c2[i];
				printf("%d\n", qry(rt[u], 1, nc, w)); break;
			case 6 :
				u = find(c1[i]); v = find(c2[i]);
				if(mul[rt[u]] > mul[rt[v]]) puts("1");
				else puts("0"); break;
			case 7 :
				u = find(c1[i]);
				printf("%d\n", sz[rt[u]]); break;
			default : break;
		}
	}
}

int main() {
	//freopen("4399.in", "r", stdin);
	//freopen("4399.out", "w", stdout);
	m = read();
	calc();
	return 0;
}