hihoCoder #1184 : 连通性二·边的双连通分量（边的双连通分量模板）

#1184 : 连通性二·边的双连通分量

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在基本的网络搭建完成后，学校为了方便管理还需要对所有的服务器进行编组，网络所的老师找到了小Hi和小Ho，希望他俩帮忙。

老师告诉小Hi和小Ho：根据现在网络的情况，我们要将服务器进行分组，对于同一个组的服务器，应当满足：当组内任意一个连接断开之后，不会影响组内服务器的连通性。在满足以上条件下，每个组内的服务器数量越多越好。

比如下面这个例子，一共有6个服务器和7条连接：

其中包含2个组，分别为{1,2,3},{4,5,6}。对{1,2,3}而言，当1-2断开后，仍然有1-3-2可以连接1和2；当2-3断开后，仍然有2-1-3可以连接2和3；当1-3断开后，仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。

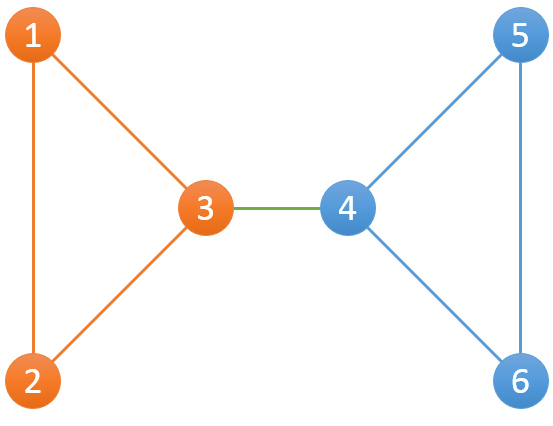
老师把整个网络的情况告诉了小Hi和小Ho，小Hi和小Ho要计算出每一台服务器的分组信息。

提示：边的双连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2个正整数，u,v。表示存在一条边(u,v)，连接了u,v两台服务器。1≤u<v≤N

保证输入所有点之间至少有一条连通路径。

输出

第1行：1个整数，表示该网络的服务器组数。

第2行：N个整数，第i个数表示第i个服务器所属组内，编号最小的服务器的编号。比如分为{1,2,3},{4,5,6}，则输出{1,1,1,4,4,4}；若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}

代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<stack>
 #include<algorithm>
 using namespace std;
 const int N=2e4+;
 vector<int>v[N];
 stack<int>sk;
 int num,cnt;
 int low[N],dfn[N],fa[N],ans[N];

 void init(){
     cnt=num=;
     memset(dfn,,sizeof(dfn));
     memset(low,,sizeof(low));
     memset(fa,,sizeof(fa));
     memset(ans,,sizeof(ans));
 }

 void dfs(int u,int f){
     low[u]=dfn[u]=++cnt;
     sk.push(u);
     for(int i=;i<v[u].size();i++){
         int t=v[u][i];
         if(!dfn[t]){
             dfs(t,u);
             low[u]=min(low[u],low[t]);
         }
         else if(t!=f) low[u]=min(low[u],dfn[t]);      //无向图不需要判断是否在栈中
     }
     // 因为low[u] == dfn[u]，对(parent[u],u)来说有dfn[u] > dfn[ parent[u] ]，因此low[u] > dfn[ parent[u] ]
     // 所以(parent[u],u)一定是一个桥，那么此时栈内在u之前入栈的点和u被该桥分割开
     // 则u和之后入栈的节点属于同一个组
     //最后剩下的一个(或者说第一个)组虽然前面没有割边，但是也适用于这个判断
     if(low[u]==dfn[u]){
         ++num;
         while(!sk.empty()){
             int t=sk.top();
             sk.pop();
             fa[t]=num;
             if(ans[num]==||ans[num]>t)
                 ans[num]=t;
             if(t==u)
                 break;
         }
     }
 }

 int main(){
     int n,m;
     while(~scanf("%d%d",&n,&m)){
         init();
         for(int i=;i<=m;i++){
             int a,b;
             scanf("%d%d",&a,&b);
             v[a].push_back(b);
             v[b].push_back(a);
         }
         dfs(,-);
         printf("%d\n",num);
         for(int i=;i<=n;i++){
             printf("%d%c",ans[fa[i]],i==n?'\n':' ');
         }
     }
     return ;
 }