hdoj 2046 骨牌铺方格 【DP】+【斐波那契】

dp果然不是好学的。。。

第n个，即2*n时，可由第n-1个的竖直排列再加一个，和第n-2个中横着排两个

所以f(n) = 1×f(n-1) + 1×f(n-2)；

骨牌铺方格

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 28412    Accepted Submission(s): 13771

Problem Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.

比如n=3时,为2× 3方格，骨牌的铺放方案有三种,例如以下图：

 

Input

输入数据由多行组成，每行包括一个整数n,表示该測试实例的长方形方格的规格是2×n (0<n<=50)。

 

Output

对于每一个測试实例。请输出铺放方案的总数，每一个实例的输出占一行。

 

Sample Input

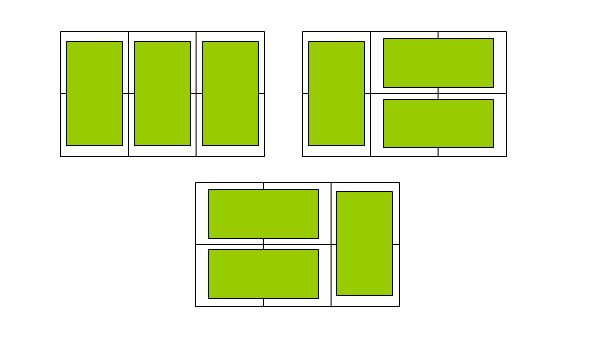
1
3
2

 

Sample Output

1
3
2

 

Author

lcy

 

代码：

#include<stdio.h>
__int64 ans[55] = {1, 1};
void f()
{
	for(int i = 2; i <54; i ++)
		ans[i] = ans[i-1]+ans[i-2];
}
int main()
{
	f();
	int n;
	while(scanf("%d", &n) == 1){
		printf("%I64d\n", ans[n]);
	}
}