Sending Secret Messages LightOJ - 1404

Sending Secret Messages LightOJ - 1404

Alice wants to send Bob some confidential messages. But their internet connection is not secured enough. As their names have been used in many networking schemes, they are very rich now. So, they don't want to send encoded messages, they want to use secured dedicated connection for them. So, they talked to some ISPS (Internet Service Providers) about their problem. Only they get is that there are N routers in the network, some of them share bidirectional links. Each link has a capacity, and for each KB of data passing through this link, they have to pay some money. Assume that Alice is connected with the 1^st router and Bob is connected to the N^th router.

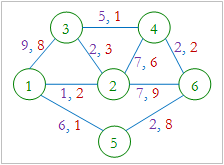
For example, in the picture, Alice wants to send 4 KB data from router 1 to router 6. Each link is identified by two integers in the form (a, b) where 'a' denotes the capacity of the link and 'b'denotes per KB cost of the link. So, Alice can send 1KB of data through 1 - 2 - 3 - 4 - 6 (cost 8), 2KB data through 1 - 5 - 6 (cost 2 * 9=18) and 1KB data through 1 - 3 - 4 - 6 (cost 11). So, the total cost is 37 units.

Now Alice wants to send P KB of data to Bob. You have to find the minimum amount of money they have to pay to achieve their goal.

Input

Input starts with an integer T (≤ 50), denoting the number of test cases.

Each case starts with a blank line. Next line contains three integers N (2 ≤ N ≤ 50), M (0 ≤ M ≤ N*(N-1)/2) and P (1 ≤ P ≤ 1000), where M denotes the number of bidirectional links. Each of the next M lines contains four integers u v w c (1 ≤ u, v ≤ N, u ≠ v, 1 ≤ w, c ≤ 100), meaning that there is a link between router u and v, and at most c KB data can be sent through this link, and each KB of data through this link will cost w. You can assume that there will be at most one connection between a pair of routers.

Output

For each case, print the case number and the minimum amount of money required or "impossible" if it's not possible to send P KB of data.

Sample Input

3

6 9 4

3 1 9 8

1 2 1 2

1 5 6 1

5 6 2 8

6 4 2 2

4 2 7 6

2 6 7 9

3 4 5 1

3 2 2 3

6 9 9

3 1 9 8

1 2 1 2

1 5 6 1

5 6 2 8

6 4 2 2

4 2 7 6

2 6 7 9

3 4 5 1

3 2 2 3

4 4 20

1 3 1 3

3 4 1 4

1 2 1 2

2 4 1 5

Sample Output

Case 1: 37

Case 2: 139

Case 3: impossible

题意：给定一个图，有n个顶点m条无向边，每条边都有容量和费用，求从1到n穿输p的数据量时的费用。

题解：费用流模板，EK算法介绍  https://blog.csdn.net/y990041769/article/details/21026445

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 using namespace std;
 typedef long long ll;
 const int MAXX=;
 const int INF=0x3f3f3f3f;

 struct node
 {
     int st;
     int to;
     int next;
     int cap;
     int cost;
 }edge[MAXX];

 int head[MAXX],tol;
 int pre[MAXX],dis[MAXX];
 bool vis[MAXX];
 int n,m,p;

 void init()
 {
     tol=;
     memset(head,-,sizeof(head));
 }

 void addedge(int u,int v,int cap,int cost)
 {
     edge[tol].st=u;
     edge[tol].to=v;
     edge[tol].cap=cap;
     edge[tol].cost=cost;
     edge[tol].next=head[u];
     head[u]=tol++;

     edge[tol].st=v;
     edge[tol].to=u;
     edge[tol].cap=;
     edge[tol].cost=-cost;
     edge[tol].next=head[v];
     head[v]=tol++;
 }

 int minCostMaxFlow(int s,int t,int p)
 {
     int cost=;
     while(p>)
     {
         queue<int> q;
         memset(dis,INF,sizeof(dis));
         memset(vis,,sizeof(vis));
         memset(pre,-,sizeof(pre));
         dis[s]=;
         vis[s]=;
         q.push(s);
         while(!q.empty())
         {
             int u=q.front(); q.pop();
             vis[u]=;
             for(int i=head[u];i!=-;i=edge[i].next)
             {
                 int to=edge[i].to;
                 if(edge[i].cap>&&dis[to]>dis[u]+edge[i].cost)
                 {
                     dis[to]=dis[u]+edge[i].cost;
                     pre[to]=i;
                     if(!vis[to])
                     {
                         vis[to]=;
                         q.push(to);
                     }
                 }
             }
         }
         if(dis[t]==INF)return -;
         int minn=p;

         for(int i=pre[t];i!=-;i=pre[edge[i].st])
             minn=min(minn,edge[i].cap);

         for(int i=pre[t];i!=-;i=pre[edge[i].st])
         {
             edge[i].cap-=minn;
             edge[i^].cap+=minn;
         }
         cost+=minn*dis[t];
         p-=minn;
     }
     return cost;
 }

 int main()
 {
     int T,x,y,z,w,cas=;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d%d",&n,&m,&p);
         init();
         for(int i=;i<=m;i++)
         {
             scanf("%d%d%d%d",&x,&y,&z,&w);
             addedge(x,y,z,w);
             addedge(y,x,z,w);
         }
         int ans=minCostMaxFlow(,n,p);
         printf("Case %d: ",cas++);
         if(ans!=-) printf("%d\n",ans);
         else printf("impossible\n");
     }
     return ;
 }