acm之图论基础

1、图的定义

图 是一个顶点集合V和一个顶点间关系的集合E组成，记G=(V,E) 
V：顶点的有限非空集合。 
E：顶点间关系的有限集合（边集）。 
存在一个结点v，可能含有多个前驱节点和后继结点。

1顶点（vertex）

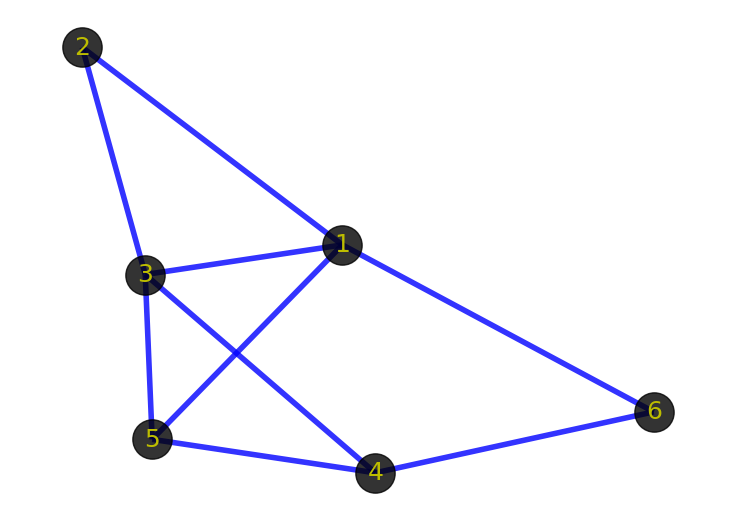
上图中黑色的带数字的点就是顶点，表示某个事物或对象。由于图的术语没有标准化，因此，称顶点为点、节点、结点、端点等都是可以的。叫什么无所谓，理解是什么才是关键。

2边（edge）

ACM图的存储（转载自剑紫青天，但是他github挂了

对于ACM图论方面的题目总是免不了首先要建图存图，使用合适的存图方式不但是AC的必要条件，解题事半功倍。

以下主要分析三种常见的存图方式的优缺点以及代码实现

• 邻接矩阵
• 邻接表
• 链式前向星

邻接矩阵

邻接矩阵是三种存图方式中最简单也最为暴力的一种存图方式了。

存图思想

使用一个矩阵来描述一个图，对于矩阵的第i行第j列的值，表示编号为i的顶点到编号为j的顶点的权值。

代码实现

对于邻接矩阵来说，它的代码实现都十分简单，二维数组就可以了。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

#include <stdio.h> #include <string.h> // 最大顶点数 const int V = 1000; // 邻接矩阵的定义 // mat[i][j] 表示 顶点`i`到顶点`j`的权值 int mat[V][V]; // 邻接矩阵的初始化操作 // 假设权值为零表示没有该边 memset(mat, 0, sizeof(mat)) // 增加边 // 新增顶点`i`到顶点`j`的边，权值为`w` mat[i][j] = w; // 删除边 // 删除顶点`i`到顶点`j`的边 mat[i][j] = 0; // 查询边 // 查询顶点`i`到顶点`j`的边权 mat[i][j];

优点

使用邻接矩阵来进行建图存图有以下优点

• 简单易学

  这个肯定不用多说，哪怕是没学过线性代数的童鞋也很容易理解这样的存图方式。

• 代码易写，简单好操作

  上面的代码实现已经展示了要定义这个数据结构以及实现初始化，增加删除边等操作有多么的简单。

• 对已确定的边进行操作，效率高

  确定边（已知两顶点编号）要进行增加或删除边（或者说更改边权）以及查询边权等操作，时间复杂度为$O(1)$。

• 易处理重边

  你可以随时覆盖掉重边，可以自己实现存储最新的边，权值最大的边或权值最小的边等。
  当然，如果你非要使用邻接矩阵存图还要存重边也不是不可以。

缺点

邻接矩阵存图虽然简单优雅，但是它的一些缺点却几乎是致命的。

• 过高的空间复杂度

  对于顶点数V，邻接矩阵存图的空间复杂度高达$O(V^2)$，顶点数上了一万可以不用考虑这种存图方式了。
  对于稀疏图来说，邻接矩阵存图内存浪费太严重，这也是邻接矩阵存图在ACM题目中十分罕见的根本原因。

• 对于不确定边的查询效率一般

  比如，我找个编号为1出发的第一条边我还要一条条边判断是否存在（权值是否为0）。

邻接表

邻接表在三种常用的存图方式中属于较为中庸和普遍的存图方式了，缺点不致命，优点不明显。

存图思想

邻接矩阵对于每个顶点使用定长的数组来存储以该点出发的边的情况。第i个数组的第j个值存储的是从顶点i到顶点j的边的权值。
而邻接表则是对于每个顶点使用不定长的链表来存储以该点出发的边的情况。因此对于第i个链表的第j个值实际上存储的是从编号为i的顶点出发的第j条边的情况。

一般来说，如果有边权的话，邻接表的链表存储的是一个结构体，这个结构体存储该边的终点以及边权。

下面给个邻接表与邻接矩阵存图的示例比较。

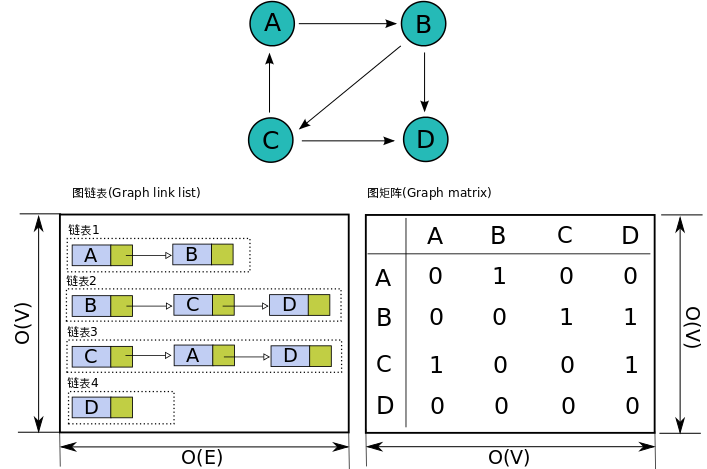
代码实现

在ACM题目中，动态的数据结构一般是不被推荐的，因为动态开辟内存比较消耗时间，且写起来复杂容易出错。
大部分情况我们使用C++STL里的vector作为链表来实现图的邻接表。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

#include <vector> using namespace std; // 最大顶点数 const int V = 100000; // vector实现的邻接表的定义 // 不考虑边权，存储类型为int型 vector<int> e[V]; // 邻接表的初始化操作 // 将起点为`i`的边链表全部清空 e[i].clear(); // 增加边 // 新增顶点`i`到顶点`j`的边 e[i].push_back(j); // 查询边 e[i][0]; // 查询以`i`为起点的第一条边`i->e[i][0]` for (int j=0; j<(int)e[i].size(); ++j) { if (e[i][j] == k) { // 查询边`i->k` // do something. } }

优点

• 较为简单易学

  相比邻接矩阵，无非是数组转链表加上存储值的意义不同而已，不需要转太大的弯。

• 代码易写，不复杂

  代码实现已经演示过了，较简单，不容易写错。

• 内存利用率较高

  对于顶点数V与边数E，空间复杂度为$O(V+E)$。能较好处理稀疏图的存储。

• 对不确定边的操作方便效率也不错

  比如，要遍历从某点出发的所有边，不会像邻接矩阵一样可能会遍历到不存在的边。

缺点

• 重边不好处理

  判重比较麻烦，还要遍历已有的边，不能直接判断。
  一般情况下使用邻接表存图是会存储重边的，不会做重边的判断。
  所以如果要解决重边的影响一般不在存边的情况下做文章。

• 对确定边的操作效率不高

  比如对于给定i->j的边要进行查询或修改等操作只有通过遍历这种方式找到了。

链式前向星

链式前向星是前向星的升级版，因为它可以完美代替前向星，所以就跳过前向星的学习，直接学习链式前向星。

存图思想

这种存图方式的数据结构主要是边集数组，顾名思义，图的边是用数组来存储的。
当然想要完美表示图结构，光有一个边集数组还不够，还要有一个数组存储指向每一个点的第一条边的“指针”。
而每一条边都需要存储接下来一条边的“指针”，这样就能够像类似邻接表一样方便遍历每一个点的所有边了。

代码实现

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

#include <stdio.h> #include <string.h> // 最大顶点数 const int V = 100000; // 最大边数 const int E = 100000; // 边结构体的定义 struct Edge { int to; // 表示这条边的另外一个顶点 int next; // 指向下一条边的数组下标，值为-1表示没有下一条边 }; // head[i] 表示顶点`i`的第一条边的数组下标，-1表示顶点`i`没有边 int head[V]; Edge edge[E]; // 链式前向星初始化，只需要初始化顶点数组就可以了 memset(head, -1, sizeof(head)); // 增加边的方式 // 新增边 a -> b，该边的数组下标为`id` inline void AddEdge(int a, int b, int id) { edge[id].to = b; edge[id].next = head[a]; // 新增的边要成为顶点`a`的第一条边，而不是最后一条边 head[a] = id; return; } // 遍历从`a`点出去的所有边 for (int i=head[a]; i!=-1; i=e[i].next) { // e[i] 就是你当前遍历的边 a -> e[i].to }

优点

• 内存利用率高

  相比vector实现的邻接表而言，可以准确开辟最多边数的内存，不像vector实现的邻接表有爆内存的风险。

• 对不确定边的操作方便效率也不错

  这点和邻接表一样，不会遍历到不存在的边。

缺点

• 难于理解，代码较复杂

  这种存图方式相对于邻接表来说比较难理解，代码虽然不是很复杂但是不熟练的话写起来也不是方便。

• 重边不好处理

  这点与邻接表一样，只有通过遍历判重。

• 对确定边的操作效率不高

  也与邻接表一样，不能通过两点马上确定边，只能遍历查找。

总结

对于邻接矩阵存图来说，由于内存消耗的局限性，它的适用范围比较狭窄，几乎只能在简单图论题目中见到。

邻接表存图是最为常见的一种，绝大部分采用C++STL中的vector实现，一般情况下大部分图论题目都能使用该存图方式。

但是链式前向星其实是一种较好替代邻接表来存图的数据结构，在邻接表存图不能使用时可以使用，几乎可以用于全部图论题目。

上图中顶点之间蓝色的线条就是边，表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系，粗细长短都无所谓的。包括上面的顶点也一样，表示逻辑事物或对象，画的时候大小形状都无所谓。

最短路是什么呢，就是两个顶点间最短的距离

floyd算法（3重循环的思行代码

    for(int k=; k<=n; k++)
        for(int i=; i<=n; i++)
            for(int j=; j<=n; j++)
                M[i][j]=min(M[i][j],M[i][k]+M[k][j]);

n条边m条路

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
int main()
{
    int n,m,M[][];
    scanf("%d%d",&n,&m);
    memset(M,INF,sizeof M);
    for(int i=; i<=n; i++)
        M[i][i]=;
    for(int i=,u,v,w; i<=m; i++)
        scanf("%d%d%d",&u,&v,&w),M[u][v]=w;
    for(int k=; k<=n; k++)
        for(int i=; i<=n; i++)
            for(int j=; j<=n; j++)
                M[i][j]=min(M[i][j],M[i][k]+M[k][j]);
    for(int i=; i<=n; i++)
    {
        for(int j=; j<=n; j++)
            printf("%d ",M[i][j]);
        printf("\n");
    }
    return ;
}

题目推荐 Stockbroker Grapevine

附录：矩阵相乘

矩阵A乘以B（15 分）

给定两个矩阵A和B，要求你计算它们的乘积矩阵AB。需要注意的是，只有规模匹配的矩阵才可以相乘。即若A有R​a​​行、C​a​​列，B有R​b​​行、C​b​​列，则只有C​a​​与R​b​​相等时，两个矩阵才能相乘。

输入格式：

输入先后给出两个矩阵A和B。对于每个矩阵，首先在一行中给出其行数R和列数C，随后R行，每行给出C个整数，以1个空格分隔，且行首尾没有多余的空格。输入保证两个矩阵的R和C都是正数，并且所有整数的绝对值不超过100。

输出格式：

若输入的两个矩阵的规模是匹配的，则按照输入的格式输出乘积矩阵AB，否则输出Error: Ca != Rb，其中Ca是A的列数，Rb是B的行数。

输入样例1：

2 3
1 2 3
4 5 6
3 4
7 8 9 0
-1 -2 -3 -4
5 6 7 8

输出样例1：

2 4
20 22 24 16
53 58 63 28

输入样例2：

3 2
38 26
43 -5
0 17
3 2
-11 57
99 68
81 72

输出样例2：

Error: 2 != 3

作者: 陈越

单位: 浙江大学

时间限制: 400ms

内存限制: 64MB

代码长度限制: 16KB

---

线代概念题

#include<bits/stdc++.h>
using namespace std;
int A[105][105],B[105][105],C[105][105];
int main()
{
    int a,b;
    cin>>a>>b;
    for(int i=0; i<a; i++)
        for(int j=0; j<b; j++)
            cin>>A[i][j];
    int c,d;
    cin>>c>>d;
    for(int i=0; i<c; i++)
        for(int j=0; j<d; j++)
            cin>>B[i][j];
    if(b!=c)
        cout<<"Error: "<<b<<" != "<<c;
    else
    {
        cout<<a<<" "<<d<<"\n";
        for(int i=0; i<a; i++)
            for(int j=0; j<d; j++)
                for(int k=0; k<b; k++)
                    C[i][j]+=A[i][k]*B[k][j];
        for(int i=0; i<a; i++)
        {
            cout<<C[i][0];
            for(int j=1; j<d; j++)
                cout<<" "<<C[i][j];
            cout<<"\n";
        }
    }
}