基于aspectj实现AOP操作的两种方式——注解方式的更多相关文章

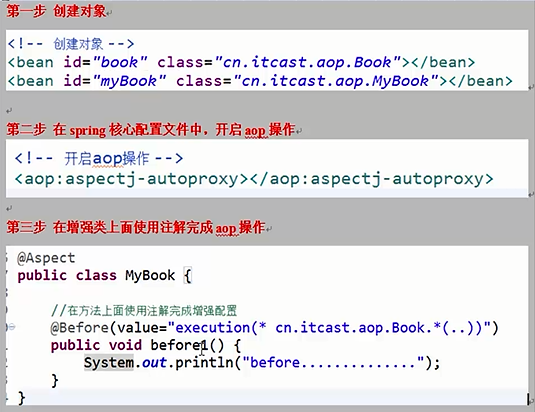
  1. 基于aspectj实现AOP操作的两种方式——xml配置

    1. 要导入的 jar 包: 常用的aspectj表达式: 权限修饰符可以省略,以下表示:返回值类型为任意,com.chy.service包以及其子包下的.任意类的.参数任意的.任意方法 execut ...

  2. spring aop提供了两种实现方式jdk和cglib

    Spring AOP使用了两种代理机制:一种是基于JDK的动态代理:另一种是基于CGLib的动态代理.之所以需要两种代理机制,很大程度上是因为JDK本身只提供接口的代理,而不支持类的代理. Sprin ...

  3. IOS文件操作的两种方式：NSFileManager操作和流操作

    1.常见的NSFileManager文件方法 -(NSData *)contentsAtPath:path //从一个文件读取数据 -(BOOL)createFileAtPath: path cont ...

  4. WCF 客户端调用服务操作的两种方法

    本节的主要内容:1.通过代理类的方式调用服务操作.2.通过通道的方式调用服务操作.3.代码下载 一.通过代理类的方式调用服务操作(两种方式添加代理类) 1.手动编写代理类,如下: 客户端契约: usi ...

  5. 利用基于@AspectJ的AOP实现权限控制

    一. AOP与@AspectJ AOP 是 Aspect Oriented Programming 的缩写,意思是面向方面的编程.我们在系统开发中可以提取出很多共性的东西作为一个 Aspect,可以理 ...

  6. Spring 基于 AspectJ 的 AOP 开发

    Spring 基于 AspectJ 的 AOP 开发 在 Spring 的 aop 代理方式中, AspectJ 才是主流. 1. AspectJ 简介 AspectJ 是一个基于 java 语言的 ...

  7. 关于vector的erase删除操作的两种不同方法，在linux与visual studio的实现讨论

    关于vector的erase删除操作的两种不同方法,在linux与visual studio的实现讨论 1.前言: 最近在做某一个题时,用到了vector的删除操作,利用的是erase()函数删除符合 ...

  8. mybatis中两种取值方式?谈谈Spring框架理解?

    1.mybatis中两种取值方式? 回答:Mybatis中取值方式有几种?各自区别是什么? Mybatis取值方式就是说在Mapper文件中获取service传过来的值的方法,总共有两种方式,通过 $ ...

  9. 牛客网Java刷题知识点之Map的两种取值方式keySet和entrySet、HashMap 、Hashtable、TreeMap、LinkedHashMap、ConcurrentHashMap 、WeakHashMap

    不多说,直接上干货! 这篇我是从整体出发去写的. 牛客网Java刷题知识点之Java 集合框架的构成.集合框架中的迭代器Iterator.集合框架中的集合接口Collection(List和Set). ...

随机推荐

  1. HashSet中存方用户自己定义数据类型数据，重写equals方法和hashCode方法

    import java.util.Set; import java.util.HashSet; public class SetTest { public static void main(Strin ...

  2. PCIE、UART、HDA、I2C、SMBUS、SPI、eSPI、USB、PS2、CAN、SDIO等数据传输协议简介

    M.2 wife一般支持USB.SDIO.PCIE三种传输 1.摄像头 (1)MIPI CSI (2)USB mipi摄像头模组IC简单便宜(小),应为一般把ADC解码在CPU端. MIPI摄像头简介 ...

  3. C#基础关键字

    1:override & new public class A { public virtual void Test() { Console.WriteLine("A Test()& ...

  4. mysql + php 中文乱码 全是？ 解决方法

    在my.ini文件中找到[client]和[mysqld]字段,在下面均加上default-character-set=utf8,保存并关闭,重启服务器 在window下重启失败,这是因为你安装了高版 ...

  5. 系统安全-PAM

    Pluggable Authentication Modules(可插入验证模块,简称PAM) Linux-PAM(Pluggable Authentication Modules for Linux ...

  6. Ipython基础功能

    ipython:交互式的python命令行 直接在终端敲命令即可进入 安装:pip install ipython 使用:在终端敲“ipython” 与python解释器的使用方法一致 TAB键自动补 ...

  7. 认识Gulp

    gulp详细入门教程:http://www.ydcss.com/archives/18 安装gulp 前提:已经安装node.js.npm $ npm install gulp --save-dev ...

  8. Dynamic Language Runtime (DLR) 初深

    本文主要包括两个内容:DLR在.Net中的位置和一次DLR的调用过程. 1. DLR在. Net 中的位置 图1 DLR 包括哪些内容? 1. Expression Tree(表达式树). 2. Dy ...

  9. java集合类学习心得

    java集合类学习心得 看了java从入门到精通的第十章,做个总结,图片均取自网络. 常用集合的继承关系 Linked 改快读慢 Array 读快改慢 Hash 两都之间 Collection是集合接 ...

  10. ickeck插件

    地址:http://www.bootcss.com/p/icheck/#skins 使用 1. 先引入文件 css <link rel="stylesheet" type=& ...