lca（最近公共祖先（在线）） 倍增法详解

转自大佬博客 ： https://blog.csdn.net/lw277232240/article/details/72870644

描述：倍增法用于很多算法当中，通过字面意思来理解

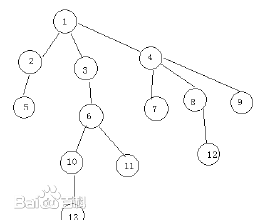
LCA是啥呢  在一棵树当中 lca表示的是两个节点最近公共祖先， 大家看这课树哈节点5 ，3的lca就是1，13和11的LCA就是6。节点8,12的lca就是8，那么我们如何通过被增来实现LCA呢。

首先请大家认真看下面的分析。

depth[x],表示x节点的深度。

大家看下这个数组 grand[x][i] ,这个数组表示标号为x节点向上跳2^i步的节点。例如grand[5][0]=2，因为5这个节点向上跳2^0次方个就是2，当然所有节点向上跳一个就是他的父亲节点，

得到grand[x][0]=他的爸爸，

那grand[x][1]=什么呢？等于grand[grand[x][0]][0];

既grand[x][i]=grand[grand[x][i-1]][i-1],为什么呢，2^4=2^3+2^3,表示 x向上跳2的i次的节点=x向上跳i-1次方的这个节点向上跳i-1次方，有点绕口。例如 grand[13][2]=grand[6][2]=g[g[rand][i-1]][i-1];

有了这个预处理那我们是不是可以得到每一个节点向上跳i格呢，然后就是i的取值范围为1<=i<=log2(n),向下取整n表示节点个数，也就是说grand[x][log2(n)]就至少可以跳到根节点甚至上面，当然上面啥都没有。

我们这里还有一个数组 gw[x][i],表示x节点向上跳2^i次方的距离（权）。同样的有gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1],这个公式表示x到他向上跳2的i次方那个节点的距离=x跳2^i-1次方的距离加上，他向上跳2^i-1次方这个点到他上面跳2^i-1次方的距离。

例如1,3,6,10,13，他们之间的边的权等于 2 4 3 6,既gw[13][0]=他爸爸10到他的距离等于6，gw[]13[2]=gw[13][1]+gw[6][1];。

其实我们可以自己加很多类似的数组

例如max[x][i]啊表示 x向上跳2^i次方的边的最大的那条边。这里就不一一举例子子了

现在有了这些预处理。我下面是用dfs实现的预处理；

就看如何实现LCA了吧，

首先 给定两个节点。假如给定的是a=13，b=12.。要我们求他们的lca ，首先第一步 我们要把他们调整到同一深度，既把a向上跳一个步这样他们的深度就相同的了。我们是把深度高的向上调。调整跟深度低的一样。

然后就两个节点一起向上跳一个2^j，首先我们j从log2(n)=3开始跳，跳到0。我们要跳到他们lca的下面两个节点。既3和4，既可以跳的节点是他们不相同并且不超出根节点(grand[a][j]!=grand[b][j])，这里是j=1的时候跳了，j=1因为(grand[a][j]!=grand[b][j]);就执行（a=grand[a][j],b=grand[b][j]）a就跳到了3,b就跳到了4，其余的j就不可以跳因为j=3，2就到根的上面了j=0他们就想等了。跳到那，最后退出，grand[a][0]就是他们的lca了。

这就是程序的执行过程。下面看代码

#include<stdio.h>
#include<string.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#define max 40001
#define maxl 25
using namespace std;
typedef struct
{
    int from,to,w;
}edge;//这个结构体用来存储边

vector<edge>edges;
vector<int> G[max];
//保存边的数组
int grand[max][maxl],gw[max][maxl];//x向上跳2^i次方的节点，x到他上面祖先2^i次方的距离
int depth[max];//深度
int n,m,N;
void addedge(int x,int y,int w)//把边保存起来的函数
{
   edge a={x,y,w},b={y,x,w};
   edges.push_back(a);
   edges.push_back(b);

   G[x].push_back(edges.size()-);
   G[y].push_back(edges.size()-);
}
void dfs(int x)//dfs建图
{
    for(int i=;i<=N;i++)//第一个几点就全部都是0咯，第二个节点就有变化了，不理解的话建议复制代码输出下这些数组

    {
        grand[x][i]=grand[grand[x][i-]][i-];
        gw[x][i]=gw[x][i-]+gw[grand[x][i-]][i-];
       // if(grand[x][i]==0) break;
    }

    for(int i=;i<G[x].size();i++)
    {   edge  e = edges[G[x][i]];
         if(e.to!=grand[x][])//这里我们保存的是双向边所以与他相连的边不是他父亲就是他儿子父亲的话就不能执行，不然就死循环了。

           {
                depth[e.to]=depth[x]+;//他儿子的深度等于他爸爸的加1
                grand[e.to][]=x;//与x相连那个节点的父亲等于x
                gw[e.to][]=e.w;//与x相连那个节点的距离等于这条边的距离
                dfs(e.to);//深搜往下面建
           }
    }
}
void Init(){
    //n为节点个数
    N = floor(log(n + 0.0) / log(2.0));//最多能跳的2^i祖先
    depth[]=;//根结点的祖先不存在，用-1表示
    memset(grand,,sizeof(grand));
    memset(gw,,sizeof(gw));
    dfs();//以1为根节点建树

}
int lca(int a,int b)
{ if(depth[a] > depth[b]) swap(a, b);//保证a在b上面，便于计算
    int ans = ;
    for(int i = N; i >= ; i--) //类似于二进制拆分，从大到小尝试
        if(depth[a] < depth[b] && depth[grand[b][i]] >= depth[a])//a在b下面且b向上跳后不会到a上面
            ans +=gw[b][i], b=grand[b][i];//先把深度较大的b往上跳

    for(int j=N;j>=;j--)//在同一高度了,他们一起向上跳,跳他们不相同节点，当全都跳完之后grand【a】【0】就是lca,上面有解释哈。
    {
        if(grand[a][j]!=grand[b][j])
        {   ans+=gw[a][j];
            ans+=gw[b][j];
            a=grand[a][j];
            b=grand[b][j];

        }
    }
    if(a!=b)//a等于b的情况就是上面土色字体的那种情况
    {
        ans+=gw[a][],ans+=gw[b][];
    }
    return ans;
}
int main()
{ int t ;
  scanf("%d",&t);
  while(t--)
  {   scanf("%d%d",&n,&m);
      for(int i=;i<n;i++)
      {
          int x,y,w;
          scanf("%d%d%d",&x,&y,&w);
          addedge(x,y,w);
      }
     Init();
     for(int i=;i<=m;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         printf("%d\n",lca(x,y));
     }
  }
}