模板<最小生成树>

转载

最小生成树浅谈

这里介绍最小生成树的两种方法：Prim和Kruskal。

两者区别：Prim在稠密图中比Kruskal优，在稀疏图中比Kruskal劣。Prim是以更新过的节点的连边找最小值，Kruskal是直接将边排序。

两者其实都是运用贪心的思路

洛谷数据：

Prim：

个人觉得Prim和最短路中的dijkstra很像，由于速度问题，所以这里我用链式前向星存图。Prim的思想是将任意节点作为根，再找出与之相邻的所有边（用一遍循环即可），再将新节点更新并以此节点作为根继续搜，维护一个数组：dis，作用为已用点到未用点的最短距离。

证明：Prim算法之所以是正确的，主要基于一个判断：对于任意一个顶点v，连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树（即任意一个属于最小生成树的连通子图，从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树）

具体算法流程图解如下：

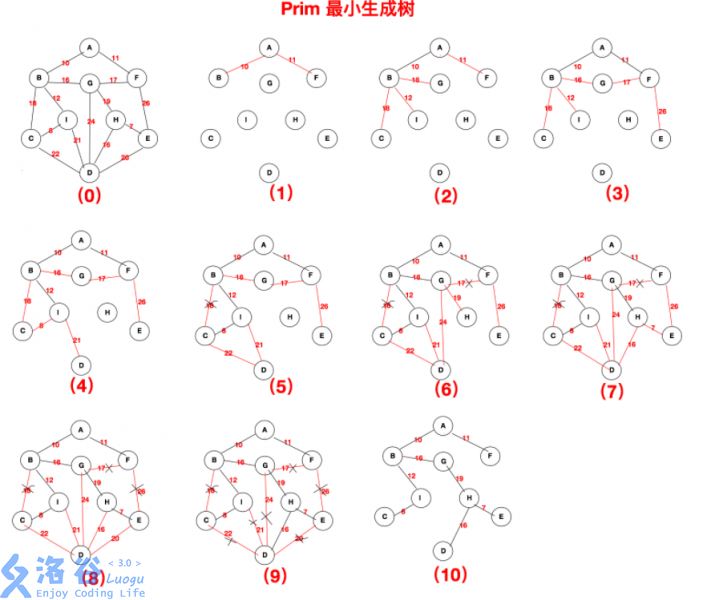
注意：inline和register为一点点常数优化，不要的话也可以过，不理解的同学删掉即可

#include<bits/stdc++.h>
using namespace std;
#define re register
#define il inline
il int read()
{
    re ,f=;char c=getchar();
    ;c=getchar();}
    )+(x<<)+(c^),c=getchar();
    return x*f;
}//快读，不理解的同学用cin代替即可
#define inf 123456789
#define maxn 5005
#define maxm 200005
struct edge
{
    int v,w,next;
}e[maxm<<];
//注意是无向图，开两倍数组
,ans;
//已经加入最小生成树的的点到没有加入的点的最短距离，比如说1和2号节点已经加入了最小生成树，那么dis[3]就等于min(1->3,2->3)
bool vis[maxn];
//链式前向星加边
il void add(int u,int v,int w)
{
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].next=head[u];
    head[u]=cnt;
}
//读入数据
il void init()
{
    n=read(),m=read();
    ,u,v,w;i<=m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w),add(v,u,w);
    }
}
il int prim()
{
    //先把dis数组附为极大值
    ;i<=n;++i)
    {
        dis[i]=inf;
    }
    //这里要注意重边，所以要用到min
    ];i;i=e[i].next)
    {
        dis[e[i].v]=min(dis[e[i].v],e[i].w);
    }
    while(++tot<n)//最小生成树边数等于点数-1
    {
        re int minn=inf;//把minn置为极大值
        vis[now]=;//标记点已经走过
        //枚举每一个没有使用的点
        //找出最小值作为新边
        //注意这里不是枚举now点的所有连边，而是1~n
        ;i<=n;++i)
        {
            if(!vis[i]&&minn>dis[i])
            {
                minn=dis[i];
                now=i;
            }
        }
        ans+=minn;
        //枚举now的所有连边，更新dis数组
        for(re int i=head[now];i;i=e[i].next)
        {
            re int v=e[i].v;
            if(dis[v]>e[i].w&&!vis[v])
            {
                dis[v]=e[i].w;
            }
        }
    }
    return ans;
}
int main()
{
    init();
    printf("%d",prim());
    ;
}

Prim

Kruskal：

Kruskal算法的思想比Prin好理解一些。先把边按照权值进行排序，用贪心的思想优先选取权值较小的边，并依次连接，若出现环则跳过此边（用并查集来判断是否存在环）继续搜，直到已经使用的边的数量比总点数少一即可。

证明：刚刚有提到：如果某个连通图属于最小生成树，那么所有从外部连接到该连通图的边中的一条最短的边必然属于最小生成树。所以不难发现，当最小生成树被拆分成彼此独立的若干个连通分量的时候，所有能够连接任意两个连通分量的边中的一条最短边必然属于最小生成树

具体算法流程图解如下：

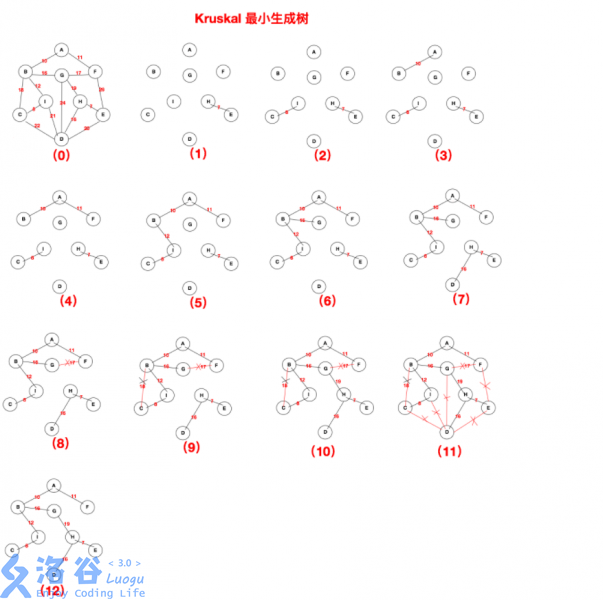
并查集详解

#include<bits/stdc++.h>
using namespace std;
#define re register
#define il inline
il int read()
{
    re ,f=;char c=getchar();
    ;c=getchar();}
    )+(x<<)+(c^),c=getchar();
    return x*f;
}
struct Edge
{
    int u,v,w;
}edge[];
],n,m,ans,eu,ev,cnt;
il bool cmp(Edge a,Edge b)
{
    return a.w<b.w;
}
//快排的依据（按边权排序）
il int find(int x)
{
    while(x!=fa[x]) x=fa[x]=fa[fa[x]];
    return x;
}
//并查集循环实现模板，及路径压缩，不懂并查集的同学可以戳一戳代码上方的“并查集详解”
il void kruskal()
{
    sort(edge,edge+m,cmp);
    //将边的权值排序
    ;i<m;i++)
    {
        eu=find(edge[i].u), ev=find(edge[i].v);
        if(eu==ev)
        {
            continue;
        }
        //若出现两个点已经联通了，则说明这一条边不需要了
        ans+=edge[i].w;
        //将此边权计入答案
        fa[ev]=eu;
        //将eu、ev合并
        )
        {
            break;
        }
        //循环结束条件，及边数为点数减一时
    }
}
int main()
{
    n=read(),m=read();
    ;i<=n;i++)
    {
        fa[i]=i;
    }
    //初始化并查集
    ;i<m;i++)
    {
        edge[i].u=read(),edge[i].v=read(),edge[i].w=read();
    }
    kruskal();
    printf("%d",ans);
    ;
}

Kruskal

PS：由于个人码风习惯，代码可能看上去较长，但其实自己写起来还是比较短的。