解题报告 之 HDU5305 Friends

解题报告 之 HDU5305 Friends

Description

There are  people
and 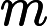 pairs
of friends. For every pair of friends, they can choose to become online friends (communicating using online applications) or offline friends (mostly using face-to-face communication). However, everyone in these 

rev=2.4-beta-2" alt="" style=""> people
wants to have the same number of online and offline friends (i.e. If one person has 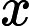 onine
friends, he or she must have 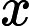 offline
friends too, but different people can have different number of online or offline friends). Please determine how many ways there are to satisfy their requirements. 

 

Input

The first line of the input is a single integer 

rev=2.4-beta-2" alt="" style="">,
indicating the number of testcases. 



For each testcase, the first line contains two integers 

rev=2.4-beta-2" alt="" style="">

rev=2.4-beta-2" alt="" style="">

rev=2.4-beta-2" alt="" style="">

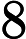
rev=2.4-beta-2" alt="" style=""> and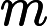 

rev=2.4-beta-2" alt="" style="">

rev=2.4-beta-2" alt="" style="">

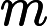
rev=2.4-beta-2" alt="" style="">

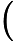
rev=2.4-beta-2" alt="" style="">,
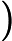
indicating the number of people and the number of pairs of friends, respectively. Each of the next 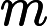 lines
contains two numbers 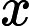 and 

rev=2.4-beta-2" alt="" style="">,
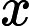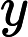which mean  and  are
friends. It is guaranteed that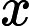 

rev=2.4-beta-2" alt="" style="">

rev=2.4-beta-2" alt="" style=""> and
every friend relationship will appear at most once. 

 

Output

For each testcase, print one number indicating the answer.

 

Sample Input

2
3 3
1 2
2 3
3 1
4 4
1 2
2 3
3 4
4 1 

 

Sample Output

0
2 

题目大意：有n个人，当中有m对朋友。既可能是网络上的朋友，也可能是现实中的朋友。如今要求每一个人网络上的朋友和现实中的朋友数量相等。但每一个人之前的朋友数量能够是不一样的，如今让你决定每一对朋友是网络朋友还是现实中的朋友来满足这个要求。问有分配方法？

分析：这道题就暴力搜索就能够了，遍历每一条边，去决定是网络朋友和现实朋友。注意剪枝假设当前边的两点中某一点的某种朋友已经超过了它关系的一半，则不用再继续搜索，由于已经不可能了。

上代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long ll;

int de[10];
int in[100], out[100];
int on[10], off[10];
int ans, m, n;

void dfs( int u )
{
	if(u == m + 1)
	{
		for(int i = 1; i <= n; i++)
		{
			if(on[i] != off[i]) return;
		}
		ans++;
		return;
	}

	if(on[in[u]] < de[in[u]] / 2 && on[out[u]] < de[out[u]]/2)
	{
		on[in[u]]++; on[out[u]]++;
		dfs( u + 1 );
		on[in[u]]--; on[out[u]]--;
	}

	if(off[in[u]] < de[in[u]] / 2 && off[out[u]] < de[out[u]]/2)
	{
		off[in[u]]++; off[out[u]]++;
		dfs( u + 1 );
		off[in[u]]--; off[out[u]]--;
	}
}

int main()
{
	int kase;

	scanf( "%d", &kase );
	while(kase--)
	{
		memset( de, 0, sizeof de );
		memset( on, 0, sizeof on );
		memset( off, 0, sizeof off );
		ans = 0;

		scanf( "%d%d", &n, &m );
		for(int i = 1; i <= m; i++)
		{
			scanf( "%d%d", &in[i], &out[i] );
			de[in[i]]++; de[out[i]]++;
		}

		int flag = true;
		for(int i = 1; i <= n; i++)
		{
			if(de[i] % 2 == 1)
			{
				printf( "0\n" );
				flag = false;
				break;
			}
		}

		if(!flag) continue;

		dfs( 1 );
		printf( "%d\n", ans );
	}
	return 0;
}