poj3233 题解 矩阵乘法 矩阵快速幂

题意：求S = A + A² + A³ + … + A^k.(mod m)

这道题很明显可以用矩阵乘法，但是这道题的矩阵是分块矩阵，

　　分块矩阵概念如下：当一个矩阵A中的单位元素aij不是一个数值而是一个矩阵是A矩阵称为分块矩阵，在性质满足的前提下依然满足矩阵加法乘法。 例如矩阵乘法A×B，将B按行分块，可以看成矩阵A乘列向量，其中B中每个元素是一个行向量；将A按列分块同理。

　　简单地说，就是矩阵里的元素还是个矩阵。这道题我们可以像这样构建矩阵：

　　　　　　　　∵S_n=S_n-1+A^k   ∴有如下转移图

　　　       　

　　　　　　　　写出邻接矩阵 （下图用E表示单位矩阵 也就是"1”，0表示全是0的矩阵 也就是“0”，A即为输入的矩阵）

　　　　　　　　

　　　　　　　　也就有：

　　　　　　　　        

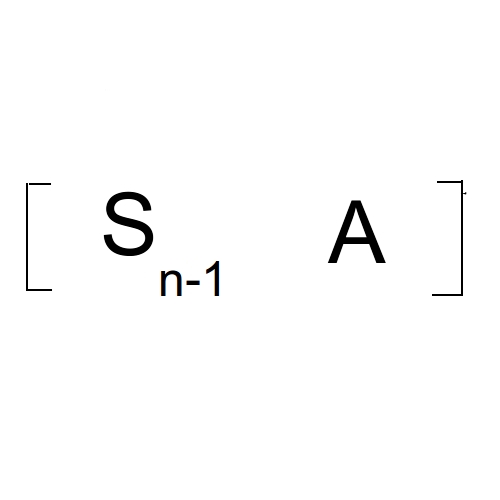
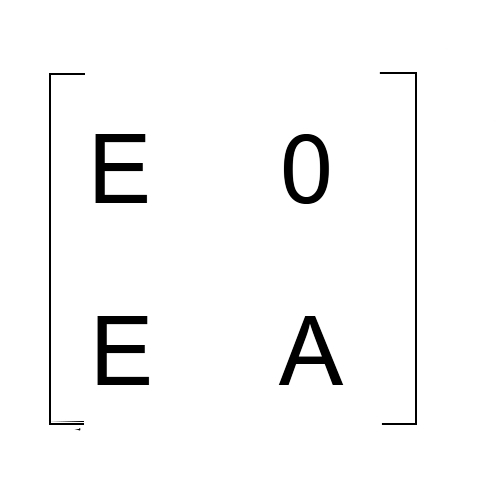
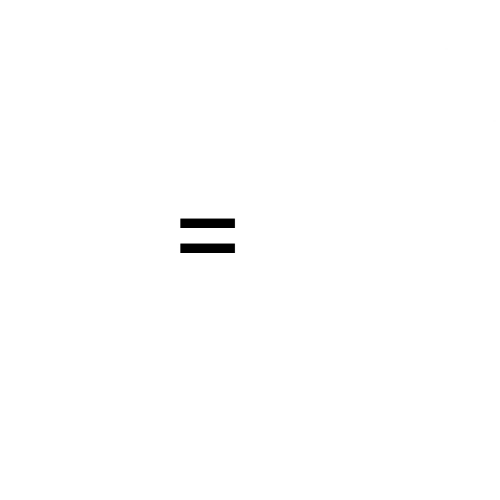
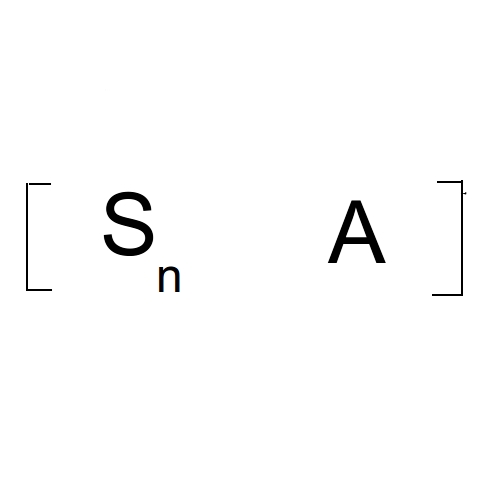
　　　　　　　　最终答案是：

　　　　　    　

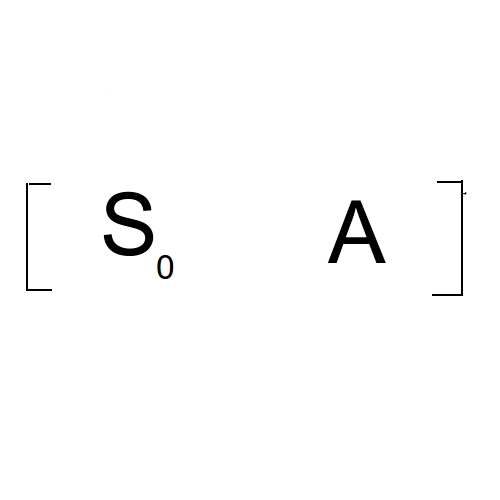
所以，最终C++程序只需要重载运算符就可以轻松AC了

而另一种做法，也就是二分加矩阵快速幂则需要较长时间（800+MS）

 #include <iostream>
 #include <algorithm>
 #include <cmath>
 #include <ctime>
 #include <cstring>
 #include <cstdio>
 #include <cstdlib>

 using namespace std;

 int    n,k,m;

 class Matrix
 {
     public:
     int    val[][];
     int    x,y;

     Matrix()
     {
         memset(val,,sizeof(val));
         x=y=;
         return ;
     }

     void    set_E()
     {
         int    i;
         for(i=;i<=x;++i)
             val[i][i]=;
         return ;
     }

     Matrix operator*(Matrix b)
     {
         int    i,j,k;
         Matrix    c;
         c.resize(x,b.y);

         for(k=;k<=b.x;++k)
         for(i=;i<=x;++i)
         if(val[i][k])//不加这行就要340+MS
         for(j=;j<=b.y;++j)
             c.val[i][j]=(c.val[i][j]+val[i][k]*b.val[k][j])%m;
         return c;
     }

     Matrix    operator+(Matrix b)
     {
         Matrix    c;
         c.resize(max(x,b.x),max(y,b.y));
         int    i,j;

         for(i=;i<=c.x;++i)
         for(j=;j<=c.y;++j)
             c.val[i][j]=(val[i][j]+b.val[i][j])%m;

         return c;
     }

     void    resize(const int & _x,const int & _y)
     {
         x=_x,y=_y;
         return ;
     }
 }A;

 class    Matrix_Plus
 {
     public:
     Matrix    val[][];
     int    x,y;

     Matrix_Plus()
     {
         memset(val,,sizeof(val));
         x=y=;
         return ;
     }

     void    set_E()
     {
         int    i;
         for(i=;i<=x;++i)
             val[i][i].set_E();
         return ;
     }

     Matrix_Plus operator*(Matrix_Plus b)
     {
         Matrix_Plus    c;
         int    i,j,k;
         c.resize(x,b.y);

         for(k=;k<=b.x;++k)
         for(i=;i<=x;++i)
         for(j=;j<=b.y;++j)
             c.val[i][j]=c.val[i][j]+val[i][k]*b.val[k][j];
         return c;
     }

     Matrix_Plus operator^(int    p)
     {
         Matrix_Plus    r,base;
         r.resize(,);
         r.val[][].resize(n,n);
         r.val[][].resize(n,n);
         r.val[][].resize(n,n);
         r.val[][].resize(n,n);
         r.set_E();
         base=*this;

         while(p)
         {
             if(p&)
                 r=r*base;
             base=base*base;
             p>>=;
         }

         return r;
     }

     void    resize(const int & _x,const int & _y)
     {
         x=_x,y=_y;
         return ;
     }

 }S,A_;

 int main()
 {
     int    i,j;

     scanf("%d%d%d",&n,&k,&m);
     A.resize(n,n);

     for(i=;i<=n;++i)
     {
         for(j=;j<=n;++j)
         {
             scanf("%d",&A.val[i][j]);
         }
     }

     S.resize(,);
     S.val[][]=A;
     S.val[][].resize(n,n);
     S.val[][].resize(n,n);

     A_.resize(,);
     A_.val[][].resize(n,n);
     A_.val[][].resize(n,n);
     A_.val[][].resize(n,n);
     A_.val[][].resize(n,n);
     A_.val[][].set_E();
     A_.val[][].set_E();
     A_.val[][]=A;
     S=S*(A_^k);

     for(i=;i<=n;++i)
     {
         for(j=;j<=n;++j)
             printf("%d ",S.val[][].val[i][j]);
         printf("\n");
     }
     return ;
 }