leetcode：Longest Palindromic Substring（求最大的回文字符串）

Question：Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.（给定一个字符串S，在S中找到最长的回文子字符串，假定最长的回文字符串长度是1000，并且在这个字符串中存在唯一的一个最长回文子字符串）

　　今天做到leetcode上的这个题，没有想到这个题也竟然是百度14年的笔试题，题目大体相同。下面我来分享一下我在做这个题的时候的一些感悟。

　　最开始，对这个题没有思路，想到一种很笨的方法，也就是穷举的思想，能够得到最长的回文子字符串，但是leetcode测试时间超时，下面是这种方法的代码（Java）

 class Solution {
     //超过leetcode时间要求
     public String longestPalindrome(String s) {
         // Note: The Solution object is instantiated only once and is reused by each test case
         String str=new String();
         int max=0;
         //穷举法是很笨的方法
         for(int i=0;i<s.length();i++){
             for(int j=i+2;j<=s.length();j++){
                 if(isPalindrome(s.substring(i,j))&&(j-i)>max){
                     str=s.substring(i,j);
                     max=j-i;
                 }
             }
         }
         return str;
     }
     //判断是否是回文字符串
     public Boolean isPalindrome(String s){
         for(int i=0;i<s.length()/2;i++){
             if(s.charAt(i)!=s.charAt(s.length()-i-1))
                 return false;
         }
         return true;
     }
 }

第二种方法思路是：首先把字符串s反转得到str1，s与str1相同的字符串就有可能是回文子字符串，之所以说有可能是因为有一种情况求出的相同字符串不是所要求的，比如s="12343943215",下面我会做详细介绍，第二种方法代码如下：

 class Solution5{
        public String longestPalindrome(String s) {
            String str=reverseNewString(s);
            return longestSubString(s, str);
        }
        /**
         * 在不改变原有字符串排列的情况下反序
         * */
        public String reverseNewString(String s){
            String str="";
            for (int i=s.length()-1;i>=0;i--) {
             str+=s.charAt(i);
         }
            return str;
        }
        /**
         * str1和str2是两个反序的字符串，他们两者中相同的最长的子字符串就是最长的回文字符串
         * */
        public String longestSubString(String str1,String str2){
            int length=str1.length();//字符串长度
            int [] array=new int[length+1]; //以空间换时间
            int max=0;//字符串最大长度
            int max_j=0;//下标记录
            for(int i=0;i<length;i++){
                for(int j=length-1;j>=0;j--){
                    if(str1.charAt(i)==str2.charAt(j)){
                        array[j+1]=array[j]+1;
                    }
                    else{
                        array[j+1]=0;
                    }
 //                   if(array[j+1]>=4){
 //                       System.out.println("大于4  "+"  "+array[j+1]+"  "+j);
 //                       System.out.println(str2.indexOf("yvvy")+"==="+str2.substring(182,186)+" "+str1.substring(760, 764));
 //                       System.out.println(str2.indexOf("cltg")+"==="+str2.substring(209, 213)+" "+str1.substring(733,737));
 //                       System.out.println(str2.substring(253,257)+" "+str1.substring(689, 693));
 //                   }
                    if(array[j+1]>max&&str2.substring(j+1-array[j+1],j+1).equals(str1.substring(length-j-1,length-j-1+array[j+1]))){
                        max=array[j+1];      //记录字符串最大长度
                        max_j=j+1;            //记录字符串最后字母位置
                    }
                }
            }
          //  System.out.println("array[695]="+str1.substring(692,696));
            if(max_j>0)
                return str2.substring(max_j-max,max_j);  //根据字符串长度max，和字符串最后的字母的位置max_j截取字符串
            else
                return null;                           //如果记录的下标为0,，返回空
        }
 }

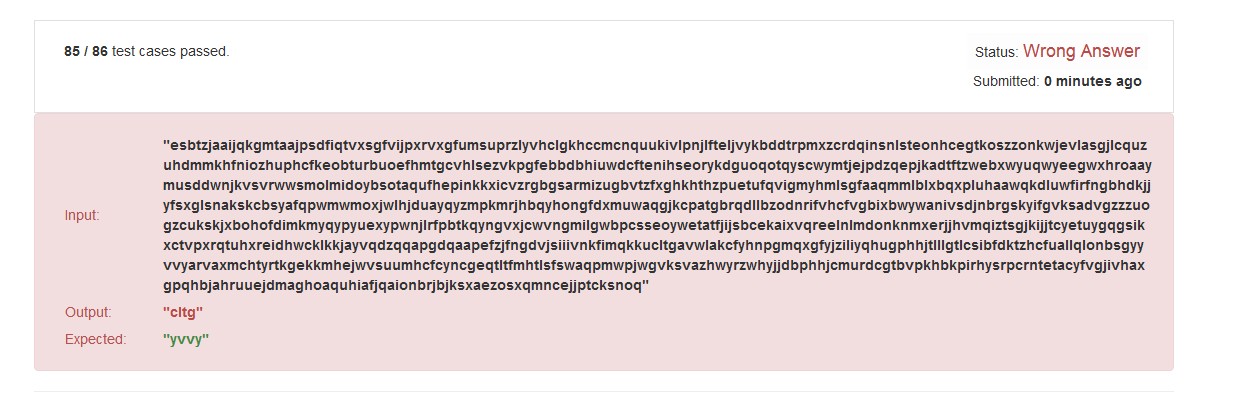
如果在代码中没有这句①str2.substring(j+1-array[j+1],j+1).equals(str1.substring(length-j-1,length-j-1+array[j+1]))，那么leetcode 测试86个案例会通过85个，那一个通不过的是哪种情况？

就是属于上边的s="12343943215"的情况，s的反转字符串str1=“51234934321”，没有上边的判断两个所要截取字符串相等的语句①，黄色数字部分比较结果会认为是相同的字符串，会输出最长回文子字符串为“1234“，”1234“肯定不是，最长应该为的为”343“。

leetcode测试没有判断语句①的情况：

leetcode测试有判断语句①的情况：

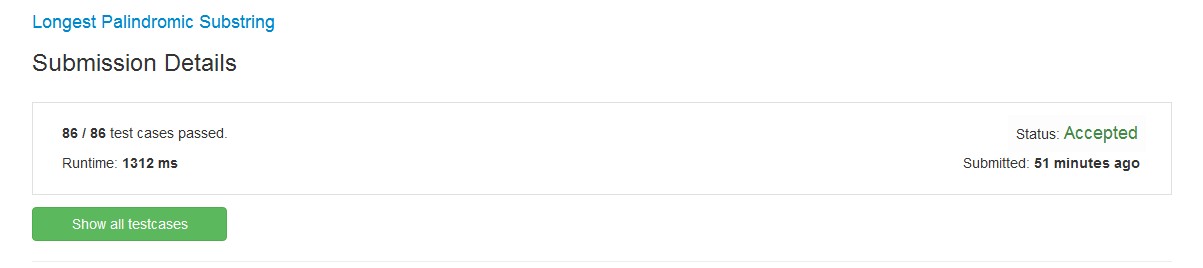
以上的第二种算法时间复杂度O（n^2）,还有更好的算法，欢迎大神吐槽，多多交流。

另外本文参照了云淡风轻kevin Lee的博客http://www.cnblogs.com/kevinLee-xjtu/archive/2011/12/21/2299082.html，并弥补了一个bug.