BZOJ 2301 Problem b

AC通道：http://www.lydsy.com/JudgeOnline/problem.php?id=2301

冬令营听了莫比乌斯，这就是宋老师上课讲的例题咯[今天来实现一下]

 #include<cstdio>
 #include<cstring>
 #include<algorithm>

 using namespace std;

 inline int in(){
     int x=;char ch=getchar();
     while(ch>'' || ch<'') ch=getchar();
     while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
     return x;
 }

 const int maxn=;

 int mu[maxn],s[maxn];
 int Prime[maxn],cnt;
 bool no_prime[maxn];

 void get_prime(){
     int tmp;mu[]=;
     for(int i=;i<maxn;i++){
         if(!no_prime[i]) Prime[++cnt]=i,mu[i]=-;
         for(int j=;j<=cnt && ((tmp=Prime[j]*i)<maxn);j++){
             no_prime[tmp]=true;
             if(i%Prime[j]==){mu[tmp]=;break;}
             mu[tmp]=-mu[i];
         }
     }
     for(int i=;i<maxn;i++) s[i]=s[i-]+mu[i];
 }

 //j表示在所有数x中n/x=n/i的最后一个
 long long calcu(int n,int m){
     long long sum=;
     if(n>m) swap(n,m);
     for(int i=,j=;i<=n;i=j+){
         j=min(n/(n/i),m/(m/i));
         sum+=(long long)(s[j]-s[i-])*(m/i)*(n/i);
     }
     return sum;
 }

 int main(){
 #ifndef ONLINE_JUDGE
     freopen("2301.in","r",stdin);
     freopen("2301.out","w",stdout);
 #endif

     int T,a,b,c,d,k;
     long long ans;

     get_prime();
     T=in();
     while(T--){
         a=in(),b=in(),c=in(),d=in(),k=in();
         ans=calcu(b/k,d/k)-calcu(b/k,(c-)/k)-calcu((a-)/k,d/k)+calcu((a-)/k,(c-)/k);
         printf("%lld\n",ans);
     }

     return ;
 }

[感觉还是说一下怎么做吧...]不过建议大家还是找个ppt来看好啦[我没有图啊...]

首先将问题变成询问[i=1...n][j=1...m]中有多少gcd(i,j)==k的数

然后其实就是[i=1...n/k][j=1...m/k]中gcd(i,j)==1的数

然后设f(n,m,k)表示[i=1...n/k][j=1...m/k]中gcd(i,j)==1的个数

g(n,m,k)表示[i=1...n/k][j=1...m/k]中gcd(i,j)是1的倍数的个数 <- 小学生都知道这个等于(n/k)*(m/k)是吧

所以这一步直接由定义推来

然后莫比乌斯反演一下

然后再把g(n,m,k)的公式带一下

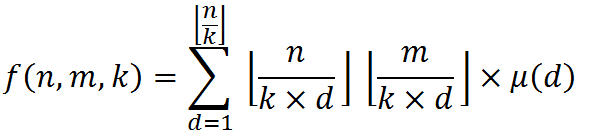
就是这个样子了...

然后发现有一大部分的数值是相同的，然后就可以看代码的分块了...