JVM内存管理--GC算法详解

标记/清除算法

　　首先，我们回想一下上一章提到的根搜索算法，它可以解决我们应该回收哪些对象的问题，但是它显然还不能承担垃圾搜集的重任，因为我们在程序（程序也就是指我们运行在JVM上的JAVA程序）运行期间如果想进行垃圾回收，就必须让GC线程与程序当中的线程互相配合，才能在不影响程序运行的前提下，顺利的将垃圾进行回收。

　　为了达到这个目的，标记/清除算法就应运而生了。它的做法是当堆中的有效内存空间（available memory）被耗尽的时候，就会停止整个程序（也被成为stop the world），然后进行两项工作，第一项则是标记，第二项则是清除。

其实这两个步骤并不是特别复杂，也很容易理解。LZ用通俗的话解释一下标记/清除算法，就是当程序运行期间，若可以使用的内存被耗尽的时候，GC线程就会被触发并将程序暂停，随后将依旧存活的对象标记一遍，最终再将堆中所有没被标记的对象全部清除掉，接下来便让程序恢复运行。

　　下面我们来看下它的缺点，其实了解完它的算法原理，它的缺点就很好理解了。

1、首先，它的缺点就是效率比较低（递归与全堆对象遍历），而且在进行GC的时候，需要停止应用程序，这会导致用户体验非常差劲，尤其对于交互式的应用程序来说简直是无法接受。试想一下，如果你玩一个网站，这个网站一个小时就挂五分钟，你还玩吗？

2、第二点主要的缺点，则是这种方式清理出来的空闲内存是不连续的，这点不难理解，我们的死亡对象都是随即的出现在内存的各个角落的，现在把它们清除之后，内存的布局自然会乱七八糟。而为了应付这一点，JVM就不得不维持一个内存的空闲列表，这又是一种开销。而且在分配数组对象的时候，寻找连续的内存空间会不太好找。

　　一个算法有缺点，高人们自然会想尽办法去完善它的。而接下来我们要介绍的两种算法，皆是在标记/清除算法的基础上优化而产生的。

复制算法

　　我们首先一起来看一下复制算法的做法，复制算法将内存划分为两个区间，在任意时间点，所有动态分配的对象都只能分配在其中一个区间（称为活动区间），而另外一个区间（称为空闲区间）则是空闲的。　　

　　当有效内存空间耗尽时，JVM将暂停程序运行，开启复制算法GC线程。接下来GC线程会将活动区间内的存活对象，全部复制到空闲区间，且严格按照内存地址依次排列，与此同时，GC线程将更新存活对象的内存引用地址指向新的内存地址。

　　此时，空闲区间已经与活动区间交换，而垃圾对象现在已经全部留在了原来的活动区间，也就是现在的空闲区间。事实上，在活动区间转换为空间区间的同时，垃圾对象已经被一次性全部回收。

　　LZ给各位绘制一幅图来说明问题，如下所示。

　　此时内存被复制算法分成了两部分，下面我们看下当复制算法的GC线程处理之后，两个区域会变成什么样子，如下所示。

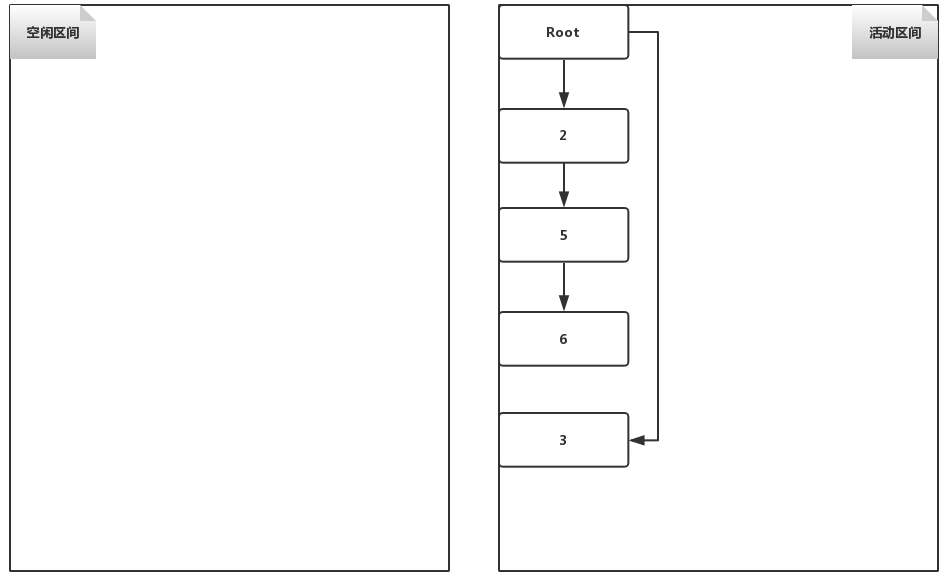
　　可以看到，1和4号对象被清除了，而2、3、5、6号对象则是规则的排列在刚才的空闲区间，也就是现在的活动区间之内。此时左半部分已经变成了空闲区间，不难想象，在下一次GC之后，左边将会再次变成活动区间。

很明显，复制算法弥补了标记/清除算法中，内存布局混乱的缺点。不过与此同时，它的缺点也是相当明显的。

1、它浪费了一半的内存，这太要命了。

2、如果对象的存活率很高，我们可以极端一点，假设是100%存活，那么我们需要将所有对象都复制一遍，并将所有引用地址重置一遍。复制这一工作所花费的时间，在对象存活率达到一定程度时，将会变的不可忽视。

所以从以上描述不难看出，复制算法要想使用，最起码对象的存活率要非常低才行，而且最重要的是，我们必须要克服50%内存的浪费。

标记/整理算法

标记/整理算法与标记/清除算法非常相似，它也是分为两个阶段：标记和整理。下面LZ给各位介绍一下这两个阶段都做了什么。

标记：它的第一个阶段与标记/清除算法是一模一样的，均是遍历GC Roots，然后将存活的对象标记。

整理：移动所有存活的对象，且按照内存地址次序依次排列，然后将末端内存地址以后的内存全部回收。因此，第二阶段才称为整理阶段。

       它GC前后的图示与复制算法的图非常相似，只不过没有了活动区间和空闲区间的区别，而过程又与标记/清除算法非常相似，我们来看GC前内存中对象的状态与布局，如下图所示。

　　

　　这张图其实与标记/清楚算法一模一样，只是LZ为了方便表示内存规则的连续排列，加了一个矩形表示内存区域。倘若此时GC线程开始工作，那么紧接着开始的就是标记阶段了。此阶段与标记/清除算法的标记阶段是一样一样的，我们看标记阶段过后对象的状态，如下图。

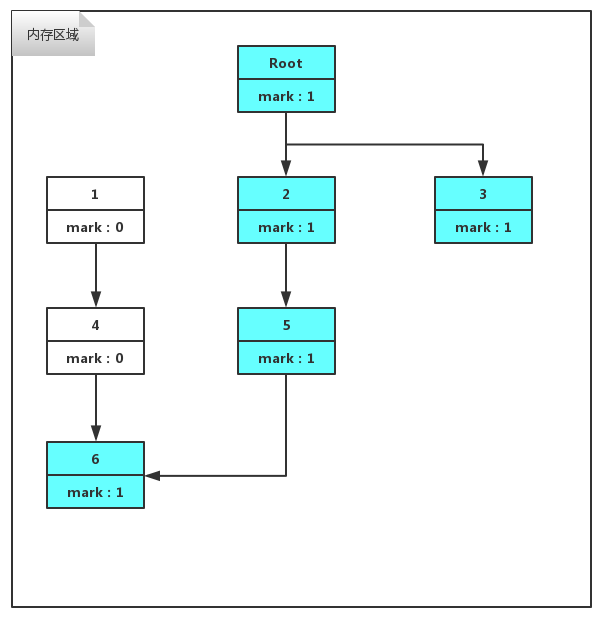
　　没什么可解释的，接下来，便应该是整理阶段了。我们来看当整理阶段处理完以后，内存的布局是如何的，如下图。

可以看到，标记的存活对象将会被整理，按照内存地址依次排列，而未被标记的内存会被清理掉。如此一来，当我们需要给新对象分配内存时，JVM只需要持有一个内存的起始地址即可，这比维护一个空闲列表显然少了许多开销。

不难看出，标记/整理算法不仅可以弥补标记/清除算法当中，内存区域分散的缺点，也消除了复制算法当中，内存减半的高额代价。

不过任何算法都会有其缺点，标记/整理算法唯一的缺点就是效率也不高，不仅要标记所有存活对象，还要整理所有存活对象的引用地址。从效率上来说，标记/整理算法要低于复制算法。

算法总结

这里LZ给各位总结一下三个算法的共同点以及它们各自的优势劣势，让各位对比一下，想必会更加清晰。

它们的共同点主要有以下两点。

       1、三个算法都基于根搜索算法去判断一个对象是否应该被回收，而支撑根搜索算法可以正常工作的理论依据，就是语法中变量作用域的相关内容。因此，要想防止内存泄露，最根本的办法就是掌握好变量作用域，而不应该使用前面内存管理杂谈一章中所提到的C/C++式内存管理方式。

       2、在GC线程开启时，或者说GC过程开始时，它们都要暂停应用程序（stop the world）。

它们的区别LZ按照下面几点来给各位展示。（>表示前者要优于后者，=表示两者效果一样）

       效率：复制算法>标记/整理算法>标记/清除算法（此处的效率只是简单的对比时间复杂度，实际情况不一定如此）。

       内存整齐度：复制算法=标记/整理算法>标记/清除算法。

       内存利用率：标记/整理算法=标记/清除算法>复制算法。