Python全栈-magedu-2018-笔记11

第三章 - Python 内置数据结构

简单选择排序

• 简单选择排序
  • 属于选择排序
  • 两两比较大小，找出极值（极大值或极小值）被放置在固定的位置，这个固定位置一般指的是某一端
  • 结果分为升序和降序排列
• 降序
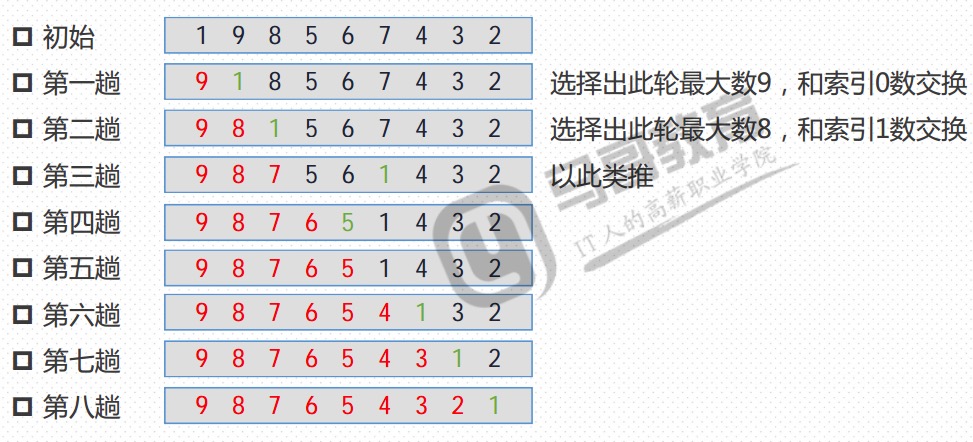
  • n个数从左至右，索引从0开始到n-1，两两依次比较，记录大值索引，此轮所有数比较完毕，将大数和索引0数交换，如果大数就是索引1，不交换。第二轮，从1开始比较，找到最大值，将它和索引1位置交换，如果它就在索引1位置则不交换。依次类推，每次左边都会固定下一个大数。
• 升序
  • 和降序相反

简单选择排序

简单选择排序代码实现（一）*

m_list = [
    [1, 9, 8, 5, 6, 7, 4, 3, 2],
    [1, 2, 3, 4, 5, 6, 7, 8, 9],
    [9, 8, 7, 6, 5, 4, 3, 2, 1]
]
nums = m_list[1]
length = len(nums)
print(nums)

count_swap = 0
count_iter = 0

for i in range(length):
    maxindex = i
    for j in range(i + 1, length):
        count_iter += 1
        if nums[maxindex] < nums[j]:
            maxindex = j

    if i != maxindex:
        tmp = nums[i]
        nums[i] = nums[maxindex]
        nums[maxindex] = tmp
        count_swap += 1

print(nums, count_swap, count_iter)

简单选择排序代码实现（二）

• 优化实现
  二元选择排序
  同时固定左边最大值和右边最小值
  优点：
  减少迭代元素的次数

  1、length//2 整除，通过几次运算就可以发现规律
  2、由于使用了负索引，所以条件中要增加
  i == length + minindex

  还有没有优化的可能？

count_swap = 0
count_iter = 0

# 二元选择排序
for i in range(length // 2):
    maxindex = i
    minindex = -i - 1
    minorigin = minindex
    for j in range(i + 1, length - i): # 每次左右都要少比较一个
    count_iter += 1
    if nums[maxindex] < nums[j]:
        maxindex = j
    if nums[minindex] > nums[-j - 1]:
        minindex = -j - 1
        # print(maxindex, minindex)

    if i != maxindex:
        tmp = nums[i]
        nums[i] = nums[maxindex]
        nums[maxindex] = tmp
        count_swap += 1
        # 如果最小值被交换过，要更新索引
        if i == minindex or i == length + minindex:
            minindex = maxindex
    if minorigin != minindex:
        tmp = nums[minorigin]
        nums[minorigin] = nums[minindex]
        nums[minindex] = tmp
        count_swap += 1

print(nums, count_swap, count_iter)

简单选择排序代码实现（二）

• 改进实现
  如果一轮比较后，极大值、极小值的值相等，说明比较的序列元素全部相等

m_list = [
    [1, 9, 8, 5, 6, 7, 4, 3, 2],
    [1, 2, 3, 4, 5, 6, 7, 8, 9],
    [9, 8, 7, 6, 5, 4, 3, 2, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1]
]

nums = m_list[3]
length = len(nums)
print(nums)
count_swap = 0
count_iter = 0
# 二元选择排序
for i in range(length // 2):
    maxindex = i
    minindex = -i - 1
    minorigin = minindex
    for j in range(i + 1, length - i): # 每次左右都要少比较一个
    count_iter += 1
    if nums[maxindex] < nums[j]:
        maxindex = j
    if nums[minindex] > nums[-j - 1]:
        minindex = -j - 1
# print(maxindex, minindex)
if nums[maxindex] == nums[minindex]: # 元素全相同
    break
if i != maxindex:
    tmp = nums[i]
    nums[i] = nums[maxindex]
    nums[maxindex] = tmp
    count_swap += 1
    # 如果最小值被交换过，要更新索引
    if i == minindex or i == length + minindex:
        minindex = maxindex
if minorigin != minindex:
    tmp = nums[minorigin]
    nums[minorigin] = nums[minindex]
    nums[minindex] = tmp
    count_swap += 1
print(nums, count_swap, count_iter)

简单选择排序代码实现（二)

• 改进实现
  [1, 1, 1, 1, 1, 1, 1, 1, 2] 这种情况，找到的最小值索引是-2，最大值索引8，上面的代码会交换2次，最小值两个1交换是无用功，所以，增加一个判断

m_list = [
    [1, 9, 8, 5, 6, 7, 4, 3, 2],
    [1, 2, 3, 4, 5, 6, 7, 8, 9],
    [9, 8, 7, 6, 5, 4, 3, 2, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 2]
]

nums = m_list[4]
length = len(nums)
print(nums)
count_swap = 0
count_iter = 0
# 二元选择排序
for i in range(length // 2):
    maxindex = i
    minindex = -i - 1
    minorigin = minindex
    for j in range(i + 1, length - i): # 每次左右都要少比较一个
        count_iter += 1
        if nums[maxindex] < nums[j]:
            maxindex = j
        if nums[minindex] > nums[-j - 1]:
            minindex = -j - 1

    print(maxindex, minindex)
    if nums[maxindex] == nums[minindex]: # 元素相同
        break
    if i != maxindex:
        tmp = nums[i]
        nums[i] = nums[maxindex]
        nums[maxindex] = tmp
        count_swap += 1
        # 如果最小值被交换过，要更新索引

        if i == minindex or i == length + minindex:
            minindex = maxindex
    # 最小值索引不同，但值相同就没有必要交换了
    if minorigin != minindex and nums[minorigin] != nums[minindex]:
        tmp = nums[minorigin]
        nums[minorigin] = nums[minindex]
        nums[minindex] = tmp
        count_swap += 1

print(nums, count_swap, count_iter)

简单选择排序总结

• 简单选择排序需要数据一轮轮比较，并在每一轮中发现极值
• 没有办法知道当前轮是否已经达到排序要求，但是可以知道极值是否在目标索引位置上
• 遍历次数1,...,n-1之和n(n-1)/2
• 时间复杂度O(n2)
• 减少了交换次数，提高了效率，性能略好于冒泡法

最后

本文的另外链接是：https://herodanny.github.io/python-magedu-2018-notes11.html