[Bayes] Metroplis Algorithm --> Gibbs Sampling
重要的是Gibbs的思想。
全概率分布,可以唯一地确定一个联合分布 ---- Hammersley-Clifford
多元高斯分布
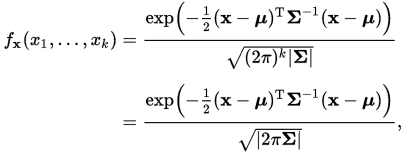
当然,这个有点复杂,考虑个简单的,二元高斯,那么超参数就是:
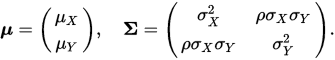
二元高斯联合分布:

将其中一个作为已知常数,也就是求条件分布,正好就体现了Gibbs的特性:

#initialize constants and parameters
N <- 5000 #length of chain
burn <- 1000 #burn-in length
X <- matrix(0, N, 2) #the chain, a bivariate sample rho <- -.75 #correlation
mu1 <- 0
mu2 <- 2
sigma1 <- 1
sigma2 <- .5
s1 <- sqrt(1-rho^2)*sigma1
s2 <- sqrt(1-rho^2)*sigma2 ###### generate the chain ##### X[1, ] <- c(mu1, mu2) #initialize for (i in 2:N) {
x2 <- X[i-1, 2]
m1 <- mu1 + rho * (x2 - mu2) * sigma1/sigma2
X[i, 1] <- rnorm(1, m1, s1)
x1 <- X[i, 1]
m2 <- mu2 + rho * (x1 - mu1) * sigma2/sigma1
X[i, 2] <- rnorm(1, m2, s2)
} b <- burn + 1
x <- X[b:N, ] # compare sample statistics to parameters
colMeans(x)
cov(x)
cor(x) plot(x, main="", cex=.5, xlab=bquote(X[1]),
ylab=bquote(X[2]), ylim=range(x[,2]))
采样结果:
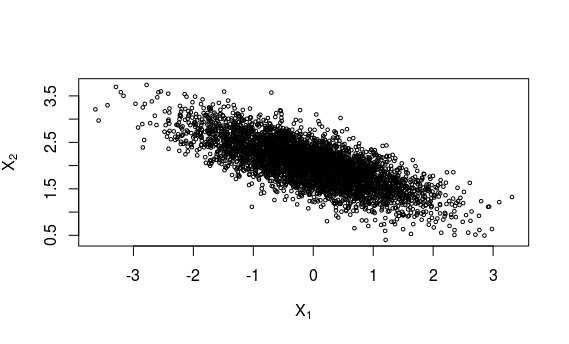
[Bayes] Metroplis Algorithm --> Gibbs Sampling的更多相关文章
- [Bayes] Hist & line: Reject Sampling and Importance Sampling
吻合度蛮高,但不光滑. > L= > K=/ > x=runif(L) > *x*(-x)^/K)) > hist(x[ind],probability=T, + xla ...
- [Bayes] Metropolis-Hastings Algorithm
[Bayes] prod: M-H: Independence Sampler for Posterior Sampling dchisq gives the density, ...
- Gibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is aMarkov chain Monte C ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling实现高斯分布参数推断
http://blog.csdn.net/pipisorry/article/details/51539739 吉布斯采样的实现问题 本文主要说明如何通过吉布斯采样来采样截断多维高斯分布的参数(已知一 ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling实现文档分类
http://blog.csdn.net/pipisorry/article/details/51525308 吉布斯采样的实现问题 本文主要说明如何通过吉布斯采样进行文档分类(聚类),当然更复杂的实 ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling
http://blog.csdn.net/pipisorry/article/details/51373090 吉布斯采样算法详解 为什么要用吉布斯采样 通俗解释一下什么是sampling. samp ...
- MCMC&Gibbs sampling
Note of Markov Chain Monte Carlo and Gibbs Sampling : http://pan.baidu.com/s/1jHpWY1o 序:A major lim ...
- 随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
随机推荐
- tomcat溢出
http://blog.csdn.net/qq_15653597/article/details/42753269?locationNum=10
- cvc-complex-type.2.4.a: Invalid content was found starting with element 'property'. One of '{"http:// www.springframework.org/schema/beans":import, "http:// www.springframework.org/schema/beans":a
因为property并未被<bean class="">标签包围, 所以要用bean标签包围即可
- mybatis学习之路----mysql批量新增数据
原文:https://blog.csdn.net/xu1916659422/article/details/77971867 接下来两节要探讨的是批量插入和批量更新,因为这两种操作在企业中也经常用到. ...
- SharePoint Online 自定义Modern UI表单
前言 用过SharePoint Online 版本的朋友们,应该很熟悉SharePoint为我们带来的Modern UI,而这个页面的订制,也跟原来的表单定制方式不同了,而且更加简单了. 而且,试了一 ...
- boost 线程安全队列
threadnullmethodsprocessingobjectsignal // QueueImplementation.cpp : Defines the entry point for the ...
- 如何自动播放光盘、解决win7电脑不能播放光盘
如何设置光盘自动播放.允许光盘自动运行呢? 在使用电脑光驱播放光盘文件的时候,经常出现的一个问题是,光驱不能自动播放光盘,但是打开光盘的文件手动操作没有任何问题,这给使用造成了很多麻烦.那么,如何让光 ...
- AWK常用技巧
1.1 介绍 awk其名称得自于它的创始人 Alfred Aho .Peter Weinberger 和 Brian Kernighan 姓氏的首个字母.实际上 AWK 的确拥有自己的语言: AWK ...
- oracle数据库将一列的值拼接成一行,并且各个值之间用逗号隔开
使用场景:把某一列值转换为逗号分隔的字符串 例子:比如查询所有的的表空间如下,现在要获得所有的表空间用逗号分隔的字符串(比如rman duplicate的时候skip表空间) SQL> sele ...
- Duplicate复制数据库并创建物理StandBy(pfile版本)
1设定环境如下: Primary数据库 IP 172.17.22.16 SID orcl Standby数据库 IP 172.17.22.17 SID orcl 设置提示,以区分操作的位置 prima ...
- 重写$.ajax方法
/*重写Jquery中的ajax 封装壳*/ $(function () { (function ($) { //首先备份下jquery的ajax方法 var _ajax = $.ajax; //重写 ...
