中位数&贪心

　　谁能想到基本算法就这么难呢？我想去冲省选，但是迟迟在这些地方 花时间 算是提升自己的思维算了。

这道题呢 答案其实很简单每个数在a的位置和在b的位置之差的累加/2即是答案为什么呢？
考虑当前数字 要向后面的那个数字换如果后面那个的目标不是当前位置呢？（自己可以把所有可能的情况画一下）

那么一定有 在当前数字的后面的目标在前面>=当前数字位置（抽屉原理）！（经过不断调整）

所以我们只需将这两个数字交换然后不断重复这个过程即是最优答案！(没有任何的浪费代价)

这个就很显然了吧，在a[(1+n)>>1]不会有任何的距离浪费，自己证明。。。（我会证明）

看减少的速率，然后画个图很显然的得出。

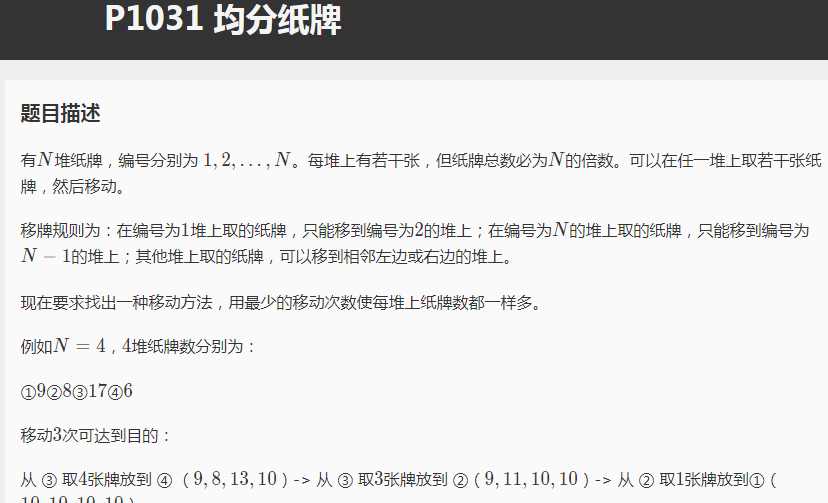
这道题就是典型的中位数的例题，那么我还是wa了（真是naocan）了

想的有点复杂本来是窥测到了证解又被自己 否定了哎

直接如果当前不够中位数的话就要旁边的那个 反正自己只能向旁边要 因为不是环啊。

那么两堆牌之间最多移动一次这样完美的解决了问题多的给旁边少的问旁边要O（n）解决。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define up(p,i,n) for(int i=p;i<=n;i++)
using namespace std;
char buf[<<],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;
}
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<?putchar('-'),x=-x:;
    int num=;char ch[];
    while(x)ch[++num]=x%+'',x/=;
    num==?putchar(''):;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const int MAXN=;
int n;
int a[MAXN],sum;
int b[MAXN],ans,cnt;
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    up(,i,n)a[i]=read(),sum+=a[i];
    //up(1,i,n)put(b[i]);
    cnt=sum/n;
    up(,i,n)a[i]-=cnt;
    up(,i,n)
    {
        if(a[i]==)continue;
        a[i+]+=a[i];
        ans++;
    }
    put(ans);
    return ;
}

这道题就是典型的中位数问题了，我还是没能窥探到正解，可能是状态不好吧。

首先我拿到题想了一个暴力n^2然后 因为问题的特异性：既然围成了一个圈子，那么其中的两个人一定不会互传糖果因为如果互传了糖果那么答案不是最优的。

且整体不能互传糖果那么答案也将不是最优的，一定有一个人只是接受糖果不再传递。但是这并不是成链的情况。

然后我们发现它还是可以具有环的性质但是 可以强行破环了，因为此时一个点一定会接收左右两个点的糖果的，然后一端传到当前点的价值<=另一端传到当前点的价值。

那么那么这一个环就自然断了，我们破环成链，从哪断呢 n^2枚举断点+累加答案。

考虑更优的做法 O(n)或者O(nlogn)显然O(n)需要一个知道一个断点才能实现，可没有任何结论不看数据的话。

那么复杂度只能是nlogn了，考虑将其都减去平均数 ，做前缀和。

因为本身如果不考虑环形的话最小代价只有一种然后ans+=|∑d[i]| d[i]=s[i]-cnt;

然后由于不知道从哪开始的d[i],我们考虑其实就是一个|前缀和d[i]|=|g[i]|

那么原式为 |g[1]|+|g[2]|+...+|g[m]| 我们能做的只能将 g数组从1~m打断然后从任何一个点开始 到达另一个点使这样短。

此时 设断点为k 那么有 ans=|g[k]-g[k-1]|+|g[k+1]-g[k-1]|+...+|g[m]-g[k-1]|+|g[1]+g[m]-g[k-1]|+...+|g[k-1]+g[m]-g[k-1]||

其实对比原式我们只是 每一项都减去了g[k-1] 仔细观察其实变化的只有k-1 因为g[m]==0;

其实原式我们可以想象成 每一个都减去了g[k-1] 然后我们只想观察g[k-1]选哪个数能使ans最小

然后这就是 数轴上一堆数字里选出一个数字使他们的差的绝对值的和最小也就是第一道题的类型了。

那个点在排序后的(n+1)>>1的位置呢，所以得到答案。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define up(p,i,n) for(long long i=p;i<=n;i++)
using namespace std;
char buf[<<],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;
}
inline long long read()
{
    long long x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
inline void put(long long x)
{
    x<?putchar('-'),x=-x:;
    long long num=;char ch[];
    while(x)ch[++num]=x%+'',x/=;
    num==?putchar(''):;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const long long MAXN=;
long long n;
long long a[MAXN],sum;
long long b[MAXN],ans,cnt,mid;
long long abs(long long x,long long y){return x>y?x-y:y-x;}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    up(,i,n)a[i]=read(),sum+=a[i];
    cnt=sum/n;
    up(,i,n)a[i]-=cnt,b[i]+=a[i]+b[i-];
    //up(1,i,n)put(b[i]);
    sort(b+,b++n);
    mid=(+n)/;
    for(long long i=;i<=n;i++)ans+=abs(b[i],b[mid]);
    put(ans);
    return ;
}

贪心：

贪心是一种在每次决策时采取当前意义下最优策略的算法

使用贪心法，要求局部最优性能够导出问题整体最优性。

贪心法通常需要证明，常见的证明手段：

1. 微扰（邻项交换）、范围缩放

2.决策包容性

3.数学归纳法、反证法

这道题呢 是一个叠罗汉问题 问题是最大的最小 考虑二分，但是呢二分出来的答案怎么验证，求出最小的的危险程度衡量mid？

等等我说求出最小rask 那么既然都求出来了为什么 还要二分 设mid为最优答案那么你一定是要验证这个mid是对的但是你这里已经把最优解求出来了。

二分变得没有那么重要了。考虑贪心的求解。

想了一小会证明出来了，但是和结训的时候证明并不一样所以。。。

不管了我是这样想的 针对 i牛,j牛 有两种 w[j]-s[j] w[i]-s[j]

所以当 w[j]-s[i]<w[i]-s[j]的时候 也就是j在上面更有优时有 w[j]+s[j]<w[i]+s[i]

利用数学归纳法可证明对于所有牛都可以这样所以排序时按照这个排序即可。

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<queue>
#include<stack>
#include<deque>
#include<map>
#include<vector>
#include<ctime>
#define INF 2147483646
#define up(p,i,n) for(int i=p;i<=n;i++)
#define ww t[i].w
#define ss t[i].s
using namespace std;
char buf[<<],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;
}
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    x<?putchar('-'),x=-x:;
    int num=;char ch[];
    while(x)ch[++num]=x%+'',x/=;
    num==?putchar(''):;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const int MAXN=;
struct wy
{
    int s,w,sum;
    friend int operator <(const wy &x,const wy &y)
    {
        return x.sum<y.sum;
    }
}t[MAXN];
int n,ans=-INF,cnt=;
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    up(,i,n)ww=read(),ss=read(),t[i].sum=ss+ww;
    sort(t+,t++n);
    for(int i=;i<=n;i++)
    {
        ans=max(ans,cnt-ss);
        cnt+=ww;
    }
    put(ans);
    return ;
}

这个呢 ？ 和上一题差不多吧不过这个要求一定要举起来维护一个二叉堆然后对排完序的罗汉们叠放

如果当前能够举起 ans++ 不能的话 找到堆中最重的 然后 比较重量如果更轻一点将其换掉。

很显然 ！因为那个更重的没有任何用处了。

还是一个最小的最大问题但我们仍不能使用二分原因和上面一样。

考虑 i j i在前 价值 a[i]/b[j] i在后 a[j]/b[i] 当 a[i]/b[j]<a[j]/b[i]时也就是i在前更优时，有 a[i]*b[i]<a[j]*b[j] 按这个从小到大排序即可。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<string>
#include<ctime>
#include<algorithm>
#include<iomanip>
#include<map>
#include<queue>
#include<stack>
#include<vector>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
struct bwy
{
    int x,y,z;
}t[];
int n,la=;
int res[maxn],ans[maxn],m[maxn],l=;
int wy(bwy x,bwy y){return x.z<y.z;}
void mul(int x)
{
    int add=;
    for(int i=;i<=l+;i++)
    {
        int tmp=m[i]*x+add;
        m[i]=tmp%;
        add=tmp/;
    }
    l+=;while(m[l]==)l--;
}
void div(int x)
{
    memset(res,,sizeof(res));
    int tmp=,u=;
    for(int i=l;i>=;i--)
    {
        tmp=tmp*+m[i];u++;
        if(tmp<x)continue;
        res[u]=tmp/x;tmp=tmp%x;
    }
    for(int i=;i<=u>>;i++)swap(res[i],res[u-i+]);
    while(res[u]==&&u>)u--;
    if(u>la){la=u;for(int i=la;i>=;i--)ans[i]=res[i];}
    else if(la==u)
    {
        int flag=;
        for(int i=la;i>=;i--){if(ans[i]<res[i])flag=;if(ans[i]>res[i])break;}
        if(flag==)for(int i=la;i>=;i--)ans[i]=res[i];
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    for(int i=;i<=n;i++){t[i].x=read();t[i].y=read();t[i].z=t[i].x*t[i].y;}
    sort(t+,t++n,wy);m[]=;
    for(int i=;i<=n;i++)
    {
        mul(t[i-].x);
        div(t[i].y);
    }
    for(int i=la;i>=;i--)printf("%d",ans[i]);
    return ;
}

但是最大值并不一定是最后一个人，因为我们只是考虑到了最优情况（整体最优所以仍需取max）。

觉得上面两道题我的分析有误

留坑 省选过后再填！