JavaScript中的算法之美——栈、队列、表

序

最近花了比较多的时间来学习前端的知识，在这个期间也看到了很多的优秀的文章，其中Aaron可能在这个算法方面算是我的启蒙，在此衷心感谢Aaron的付出和奉献，同时自己也会坚定的走前人这种无私奉献的分享精神，为编程爱好者提供一些优秀的文章

JavaScript中的栈实现

要说到栈，这里我们先将一下什么是栈，栈就是一个在计算机中特殊的数据列表，栈的特点是先进的数据最后才会被弹出来

在JavaScript中提供了可操作的方法， 入栈push,出栈pop,最先进入要最后才会弹出

栈的实现原理图大致如下，我们可以将栈理解为一个抽象的模型

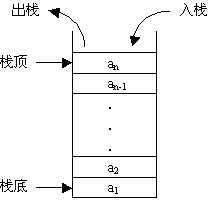
接下来我们就来讲解一下JavaScript的代码实现

1、首先我们要创建一个栈的类

2、一般对于数据结构我们是要实现增、删、改、查的功能。但是对于栈来说，改这个功能是不必要实现的，因为栈由于是连续的且后进先出等因素，所以栈是没法修改的，也就是要实现增、删、查这几个功能，还要实现清空、获取栈的长度这两个功能，同时还要引入栈顶这个参数来作为栈的变化的参考标准

空栈的实现

第一种方法是直接将直接将一个function嵌套到另外一个function中，也就是第一个function相当于类，第二个function相当于方法，再结合深入学习JavaScript（二）中的知识，我们可以构建一个有public,private概念的栈

function Stack(){
    this.dataStore = []
    this.top    = 0;
    this.push   = push;
    this.pop    = pop;
    this.peek   = peek;
    this.length = length;
    return{
        top:top,
        push:push,
        pop:pop,
        peek:peek,
        length:length
    }
}

function push(element){
    this.dataStore[this.top++] = element;
}

function peek(element){
    return this.dataStore[this.top-1];
}

function pop(){
    return this.dataStore[--this.top];
}

function clear(){
    this.top = 0
}

function length(){
    return this.top
}

要注意在这里面为了保证主函数的简洁，所以将其他的一些方法的实现封装在函数的外部然后再去调用

第二种方法是通过继承的方式来实现的

function Stack(){
    this.dataStore = []
    this.top    = 0;

}

Stack.prototype.push=function(element){
    this.dataStore[this.top++] = element;
}

Stack.prototype.peek=function (element){
    return this.dataStore[this.top-1];
}

Stack.prototype.pop=function (){
    return this.dataStore[--this.top];
}

Stack.prototype.clear=function (){
    this.top = 0
}

Stack.prototype.length=function (){
    return this.top
}

这种方法没法实现像第一种方法一样可以保证方法的封闭性

由于栈的特性是先进后出，所以利用这个特性我们可以对数组来进行倒序相关的操作，比较典型的是回文

回文

回文指的是不论是从后往前还是从前往后得到的结构都是相同的

下面我们就来通过栈实现判断字符串是否为回文

完整的代码如下：

function Stack(){
    this.dataStore = []
    this.top    = 0;
    this.push   = push
    this.pop    = pop
    this.peek   = peek
    this.length = length;
}

function push(element){
    this.dataStore[this.top++] = element;
}

function peek(element){
    return this.dataStore[this.top-1];
}

function pop(){
    return this.dataStore[--this.top];
}

function clear(){
    this.top = 0
}

function length(){
    return this.top
}
function isPalindrome(word){
    var s=new Stack();
    for(var i=0,len=word.length;i<len;i++){
        s.push(word[i]);
    }
    var rstring="";
    while(s.length()>0){
        rstring+=s.pop();
    }
    if(rstring===word){
        return true;
    }else{
        return false;
    }
}
isPalindrome("123");  //false
isPalindrome("12321");  //true

JavaScript中的队列实现

队列是只允许在一端进行插入操作，另一个进行删除操作的线性表，队列是一种先进先出（First-In-First-Out，FIFO）的数据结构

队列的实现思路跟栈的实现思路基本上是一样的，所以我们在这里就直接贴出代码就行了

function Queue() {
    this.dataStore = [];
    this.enqueue   = enqueue;
    this.dequeue   = dequeue;
    this.first     = first;
    this.end       = end;
    this.toString  = toString;
    this.empty     = empty;
}

///////////////////////////
// enqueue()方法向队尾添加一个元素： //
///////////////////////////
function enqueue(element) {
    this.dataStore.push(element);
}

/////////////////////////
// dequeue()方法删除队首的元素： //
/////////////////////////
function dequeue() {
    return this.dataStore.shift();
}

/////////////////////////
// 可以使用如下方法读取队首和队尾的元素： //
/////////////////////////
function first() {
    return this.dataStore[0];
}

function end() {
    return this.dataStore[this.dataStore.length - 1];
}

/////////////////////////////
// toString()方法显示队列内的所有元素 //
/////////////////////////////
function toString() {
    var retStr = "";
    for (var i = 0; i < this.dataStore.length; ++i) {
        retStr += this.dataStore[i] + "\n";
    }
    return retStr;
}

////////////////////////
// 需要一个方法判断队列是否为空 //
////////////////////////
function empty() {
    if (this.dataStore.length == 0) {
        return true;
    } else {
        return false;
    }
}

var q = new Queue();
q.enqueue("Aaron1");
q.enqueue("Aaron2");
q.enqueue("Aaron3");

console.log("队列头: " + q.first());   //("Aaron1");
console.log("队列尾: " + q.end());  //("Aaron3");

JavaScript中的表结构实现

虽然在JavaScript中的栈和队列都是基于数组来实现的，所以在删除元素的时候，都会涉及到对其他元素的影响，但是不论是什么语言，队列和栈都有一个十分令人讨厌的特点，不能在中间的某个位置上添加元素，这个时候我们就需要用到表结构来解决问题了

链表一般有，单链表、静态链表、循环链表、双向链表

单链表：就是很单一的向下传递，每一个节点只记录下一个节点的信息，就跟无间道中的梁朝伟一样做卧底都是通过中间人上线与下线联系，一旦中间人断了，那么就无法证明自己的身份了，所以片尾有一句话："我是好人，谁知道呢？”

静态链表：就是用数组描述的链表。也就是数组中每一个下表都是一个“节”包含了数据与指向

循环链表：由于单链表的只会往后方传递，所以到达尾部的时候，要回溯到首部会非常麻烦，所以把尾部节的链与头连接起来形成循环

双向链表：针对单链表的优化，让每一个节都能知道前后是谁，所以除了后指针域还会存在一个前指针域，这样提高了查找的效率，不过带来了一些在设计上的复杂度，总体来说就是空间换时间了

单链表，单链表的实现，我们可以看成是一个对象(包括数据+地址)，然后把这一个对象指向另外一个对象（也就是把上一个对象传递给下一个对象），这样重复下去，也就实现了我们所说的单链表，由于地址的定义是指向下一个数据的地址，但是在未添加数据的时候，我们是不知道下一个数据地址的， 所以为了克服这个问题我们可以换个思路，虽然是这样定义的，但是如果我们从后往上看，一级一级的指向上一个地址，也就是把当前链赋予下级。好了，我们来按照这个思路来实现单链表

function LinkList(){
    var data={},
        prev=null;
    return{
        add:function(val){
        prev={
            data:val,
            previous:prev||null
        }
        }
    }
}
var link=LinkList();
link.add("a1");
link.add("a2");
link.add("a3");

插入节点

上面说了链表的结构对于插入数据比较方便，所以我们就来介绍一下节点的插入，节点的插入思路是：先创建一个孤立的节点，然后是遍历链表中是否存在我们所需要的data，如果没有就在最后面插入，如果有的话就在查找到的节点后面插入，在这里我们应该关注的是链表的结构，这里我们生成的链表的结构在思想上有点像递归思想

//创建节
function createNode(data) {
    this.data = data;
    this.next = null;
}
//初始化头部节
//从headNode开始形成一条链条
//通过next衔接
var headNode = new createNode("head");

//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
    return function(key){
        //循环找到执行的节，如果没有返回本身
        while (currNode.data != key) {
            currNode = currNode.next;
        }
        return currNode;
    }
}(headNode);

//插入一个新节
this.insert = function(data, key) {
    //创建一个新节
    var newNode = new createNode(data);
    //在链条中找到对应的数据节
    //然后把新加入的挂进去
    var current = findNode(key);
    //插入新的接，更改引用关系
    //1:a-b-c-d
    //2:a-b-n-c-d
    newNode.next = current.next;
    current.next = newNode;
};

其中最为关键的代码如下所示，这一段代码是我看过的最为精辟的代码，下面我们就来分析一下

//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
    return function(key){
        //循环找到执行的节，如果没有返回本身
        while (currNode.data != key) {
            currNode = currNode.next;
        }
        return currNode;
    }
}(headNode);

其中我们为了确定链表的开头，我们先定义了一个headNode的节点，然后是将一个key传进来，注意的是传进来的Key会被初始化为节点，因为方法中是有自执行的，且已经传入了headNode节点，所以传入的格式也被确定了，这个时候currNode会等于headNode+currNode

如图所示：

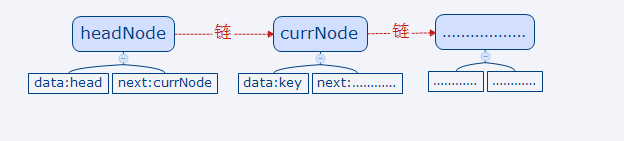
为什么为这样？因为headNode是一个全局变量，可以用来储存每次添加的节点，然而由于currNode也是一个全局变量并且通过currNode=currNode.next;所以会获取上一个节点的的位置，所以不论插入第几个对象都只循环两次，一次是上一个对象，另一次是这个对象，这个调试一下就清楚了

 文章在这里特别感谢：Aaron