ACM-ICPC 2018 南京赛区网络预赛B

题目链接：https://nanti.jisuanke.com/t/30991

Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 3030 Yuan).

However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.

The wall is covered by square ceramic tiles, which can be regarded as a n * mn∗m grid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.

For example, the following 3 * 33∗3 wall contains 3636 rectangles:

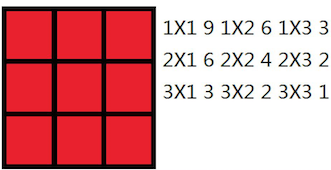
Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.

Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.

Input

There are multiple test cases in the input data.

The first line contains a integer TT : number of test cases. T \le 5T≤5.

For each test case, the first line contains 33 integers n , m , kn,m,k , denoting that the wall is a n \times mn×m grid, and the number of the black tiles is kk.

For the next kk lines, each line contains 22 integers: x\ yx y ,denoting a black tile is on the xx-th row and yy-th column. It's guaranteed that all the positions of the black tiles are distinct.

For all the test cases,

1 \le n \le 10^5,1\le m \le 1001≤n≤105,1≤m≤100,

0 \le k \le 10^5 , 1 \le x \le n, 1 \le y \le m0≤k≤105,1≤x≤n,1≤y≤m.

It's guaranteed that at most 22 test cases satisfy that n \ge 20000n≥20000.

Output

For each test case, print "Case #xx: ansans" (without quotes) in a single line, where xx is the test case number and ansans is the answer for this test case.

Hint

The second test case looks as follows:

样例输入复制

样例输出复制

Case #1: 36

Case #2: 20

题目来源

ACM-ICPC 2018 南京赛区网络预赛

题意：给你一个长方形的方格图，要你找出图中的小方块可以组成矩形的最大个数，黑色方块不能参与矩形的组成，

先输入一个整数T代表样例的个数，接下来分别给出T个样例，对于每一个样例，输入三个数字a，b，c。a，b分别代表长方形方格图的长宽，c代表黑色方格的数量，下来c行每行输入两个整数x，y，代表黑色方格的位置，

思路：这题在比赛的时候看都没有看，也觉得直接写不出，赛后学长给我们讲了一种极其精妙的思路。。。。。

先看代码吧。。。。

#include<cstdio>

#include<cstring>

#define ll long long

using namespace std;

bool s[100010][110];

int l[110];

int main(){

	int t;

	int x,y;

	int n,m;

	int i,j,k;

	int up,mn,cnt;

	ll ans;

	cnt=0;

	scanf("%d",&t);

	while(t--){

		ans=0;

		cnt++;

		memset(s,false,sizeof(s));

		memset(l,0,sizeof(l));

		scanf("%d%d%d",&n,&m,&k);

		while(k--){

			scanf("%d%d",&x,&y);

			s[x][y]=true;

		}

		for(i=1;i<=n;i++){

			up=0;//一列中可以到达的下限位置

			for(j=1;j<=m;j++){//一列的开始位置

				if(s[i][j]){//该坐标为黑更新该列的下限位置和该行的左极限

					l[j]=i;

					up=j;

				}

				mn=i-l[j];

				for(k=j;k>up;k--){

					if(mn>(i-l[k]))//更新组成新矩形左边可以到的最大位置

					mn=i-l[k];

					ans+=mn;//该位置可以新增矩阵的数量为左边可以到达的最大值

				}

			}

		}

		printf("Case #%d: %lld\n",cnt,ans);

	}

}

可能你刚看到代码的时候会一脸疑惑，这到底是怎么写的，因为我本人的水平太低，可能写在字面上的解释会不太清除。。。。我先把这道题目的核心代码解释一下

for(k=j;k>up;k--){

					if(mn>(i-l[k]))//更新组成新矩形左边可以到的最大位置

					mn=i-l[k];

					ans+=mn;//该位置可以新增矩阵的数量为左边可以到达的最大值

				}

　　这一段代码就是用来计算可以组成矩形的数量的

我们是以计算以当前位置为基底来计算可以新增矩行的数量

可能这有点难以理解

我们有三个for循环来解决这道题目

第一个循环为1----n

第二个循环为1----m

行为n

列为m

我们计算矩形时是按照先从（1，1）位置开始计算，一直顺序计算到（1，m），然后再从（2，1）位置开始计算，一直顺序计算到（2，m）。。。。。。直到计算到（n，m）位置停止，

对于每次可以新增的矩形数量，我们就可以计算为从当前位置（当前方格块一定为新方格块），以增加已经遍历过的旧的方格的方法来创建新矩形。至于新矩形的计算

字丑请不要介意